games101 一、变换和光栅化

变换（Transform）

有几种常见的变换

缩放（Scale）
翻转（Reflection）
切变（Shear）
旋转（Rotate）

旋转（Rotate）

旋转矩阵

\[ \begin{bmatrix} \cos\theta & -\sin\theta\\ \sin\theta & \cos\theta \end{bmatrix} \]

一个结论：旋转矩阵的逆矩阵等于它的转置矩阵（我们把这样的矩阵称为正交矩阵），即

\[ R^{-1} = R^T \]

切变（Shear）

以下是一个x方向上切变的例子（这是一个2维变换）

变换前

   ^ y
   |
 1 | +-----+
   | |     |
 0 | +-----+
   +--------------> x

变换后

   ^ y
   |
 1 |    /-----/      ← 顶边向右平移 k
   |   /     /
 0 | +-----/
   +--------------> x

表示为矩阵乘法：

\[ \begin{bmatrix} x'\\ y' \end{bmatrix} = \begin{bmatrix} 1 & a\\ 0 & 1 \end{bmatrix} \begin{bmatrix} x\\ y \end{bmatrix} \]

齐次坐标（Homogeneous Coordinates）和仿射变换（Affine Transformation）

（下面以2维变换为例来说明这个问题）

齐次坐标（Homogeneous Coordinates）

齐次坐标的引入是为了解决线性变换无法表示平移的问题，没有齐次坐标的情况下，一个带有平移的变化必须表示为以下形式：

\[ \vec{y} = A\vec{x} + \vec{b} \]

展开为：

\[ \begin{bmatrix} x'\\ y' \end{bmatrix} = \begin{bmatrix} a & b\\ c & d \end{bmatrix} \begin{bmatrix} x\\ y \end{bmatrix} + \begin{bmatrix} t_x\\ t_y \end{bmatrix} \]

为了简化表示和计算，我们引入齐次坐标，将二维向量扩展为三维向量：

将二维的点 $(x, y)$ 扩展为 $(x, y, 1)$
将二维的向量 $(x, y)$ 扩展为 $(x, y, 0)$

以下是一个利用齐次坐标对一个点做平移变换的例子：

\[ \begin{pmatrix} x'\\ y'\\ w' \end{pmatrix} = \begin{pmatrix} 1 & 0 & t_x\\ 0 & 1 & t_y\\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x\\ y\\ 1 \end{pmatrix} = \begin{pmatrix} x+t_x\\ y+t_y\\ 1 \end{pmatrix} \]

为什么向量的第三维是0呢？是因为向量具有平移不变性，如果是对一个向量做变换，为了使向量不受平移变换的影响，它的第三维必须是0。

在这个定义下（点的第三维是1，向量的第三维是0），以下这些操作都是有效的：

vector + vector = vector
point - point = vector
point + vector = point
point + point = ??

对于第四种情况，由于两个点相加后，第三维变成了2，不再符合齐次坐标的定义，因此，人们对这种情况做了扩充，规定：

\[ \begin{pmatrix} x\\ y\\ w \end{pmatrix} \text{ is the 2D point } \begin{pmatrix} x/w\\ y/w\\ 1 \end{pmatrix}, \quad w\neq 0 \]

其实就是两个点相加的结果是这两个点的中点

这也意味着，我们对齐次坐标下的一个点的4个维度都乘以一个数k，它和原来的点是同一个点，后面的透视投影会用到这个性质。

仿射变换（Affine Transformation）

上面提到的线性变换+平移（Translation）的组合叫做仿射变换

\[ \begin{bmatrix} x'\\ y' \end{bmatrix} = \begin{bmatrix} a & b\\ c & d \end{bmatrix} \begin{bmatrix} x\\ y \end{bmatrix} + \begin{bmatrix} t_x\\ t_y \end{bmatrix} \]

利用齐次坐标，可以将仿射变换表示为矩阵乘法：

\[ \begin{pmatrix} x'\\ y'\\ 1 \end{pmatrix} = \begin{pmatrix} a & b & t_x\\ c & d & t_y\\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x\\ y\\ 1 \end{pmatrix} \]

3维变换

将齐次坐标引入3维空间可得3维变换，其基本形式为：

\[ \begin{pmatrix} x'\\ y'\\ z'\\ 1 \end{pmatrix} = \begin{pmatrix} a & b & c & t_x\\ d & e & f & t_y\\ g & h & i & t_z\\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x\\ y\\ z\\ 1 \end{pmatrix} \]

3维旋转

欧拉角旋转

将任意一个3维旋转分解为绕x轴、y轴、z轴的旋转的组合

\[ \vec{R}_{xyz}(\alpha,\beta,\gamma) = \vec{R}_x(\alpha)\,\vec{R}_y(\beta)\,\vec{R}_z(\gamma) \]

$\alpha$、$\beta$、$\gamma$又称为欧拉角（Euler Angles）

这三种旋转类似飞机的滚转（Roll）、俯仰（Pitch）、偏航（Yaw）

欧拉角旋转变换不太方便做插值，四元数变换可以解决这个问题。

罗德里格斯旋转公式（Rodrigues' rotation formula）

将绕任意过原点的轴 $\vec{n}=(n_x,n_y,n_z)$ 旋转 $\alpha$ 角度的旋转矩阵表示为以下形式（其中，$\vec{I}$ 是单位矩阵）：

\[ \vec{R}(\vec{n},\alpha) = \cos(\alpha)\,\vec{I} + \bigl(1-\cos(\alpha)\bigr)\,\vec{n}\,\vec{n}^{\mathsf T} + \sin(\alpha)\, \underbrace{\begin{pmatrix} 0 & -n_z & n_y\\ n_z & 0 & -n_x\\ -n_y & n_x & 0 \end{pmatrix}}_{\vec{N}} \]

四元数旋转

四元数是一种代数结构，可以用来表示3维空间中的旋转。

和罗德里格斯公式一样，四元数旋转同样是表示绕任意过原点的轴 $\vec{n}=(n_x,n_y,n_z)$ 旋转 $\alpha$ 角度。

这里给出四元数的基本形式:

\[ \vec{q} = x i + y j + z k + w \]

简记为：

\[ \vec{q} = (u, w) \]

纯四元数是指把一个向量 $(x, y, z)$ 表示为四元数的形式：

\[\vec{v} = (v, 0) = x i + y j + z k + 0\]

这里省略四元数的性质和运算规则。

以下是四元数旋转的公式：

\[ R_q(\vec{v}) = q\,\vec{v}\,q^{-1} = q\,\vec{v}\,q^{\star} = \cos(2\theta)\,\vec{v} + \bigl(1-\cos(2\theta)\bigr)\,(\vec{n}\!\cdot\!\vec{v})\,\vec{n} + \sin(2\theta)\,(\vec{n}\!\times\!\vec{v}) \]

$R_q(\vec{v})$ 将向量绕轴 $\vec{n}$ 旋转 $2\theta$ 角度，$\vec{v}$是把向量表示为纯四元数的形式（$q^{\star}$ 是四元数 $q$ 的共轭四元数。$q^{-1}$ 是四元数 $q$ 的逆四元数）

为了最终旋转的角度是 $\theta$，我们需要将四元数定义为：

\[q = \left(\sin(\theta/2)\vec{n}, \cos(\theta/2)\right)\]

计算结果也是个纯四元数，等价于向量

欧拉角

欧拉角是一种三维姿态的描述方法，它表示的是按某种固定顺序的三次旋转动作。

欧拉角按照旋转轴和旋转顺序分为经典欧拉角（Proper Euler Angle）和泰特布莱恩角（Tait–Bryan angles），共 12种旋转方式。

经典欧拉角只绕两个轴旋转，并且第一个旋转轴和第三个旋转轴相同，它的六种旋转顺序分别是：z-x-z, x-y-x, y-z-y, z-y-z, x-z-x, y-x-y

泰特-布莱恩角使用三个旋转轴，它的六种旋转顺序分别是：x-y-z, y-z-x, z-x-y, x-z-y, z-y-x, y-x-z

按照旋转的坐标系分为两种旋转方式：

内旋（intrinsic rotation），是每次都相对于变换后的坐标系（即自身的、本地的坐标系）做旋转，又叫动态旋转。

外旋（extrinsic rotation），是每次都相对初始的（固定的）坐标系做变换，又叫静态旋转。

内旋和外旋有一种等价关系，例如，内旋 z-x-y 等价于外旋 y-x-z，特点是第一次和最后一次旋转的轴颠倒了顺序，这个关系对12种旋转方式都成立。

万向节死锁（Gimbal Lock）问题

对于泰特布莱恩角（Tait–Bryan angles），例如，以x-y-z 外旋为例，当绕y轴旋转90度后，这时绕z轴旋转和最开始绕x轴的旋转实际上造成的效果是相同的，这是一种万向节死锁（Gimbal Lock）现象。

对于经典欧拉角（Proper Euler Angle），例如，以z-x-z 外旋为例，当绕x轴旋转0度或180度后，这时绕z轴旋转和最开始绕z轴的旋转实际上造成的效果是相同的，这也是一种万向节死锁（Gimbal Lock）现象。

网上有很多拿万向陀螺仪来解释这个问题的文章，毫无疑问，全是错误的，万向陀螺仪的万向节死锁问题和欧拉角的万向节死锁问题是两个完全不同的概念，万向陀螺仪的万向节死锁问题是因为机械结构的限制而产生的旋转自由度受限问题，而欧拉角的万向节死锁问题是由特殊旋转顺序和角度组合导致的旋转冗余问题。

观测变换（Viewing Transformation）

主要内容：

View (视图) / Camera transformation
Projection (投影) transformation
- Orthographic (正交) projection
- Perspective (透视) projection

渲染一个场景总共需要3步

Model transformation：把场景搭建好
View transformation：找个拍摄角度，把场景放到摄像机前面
Projection transformation：拍照！把3D场景投影到2D平面上

这三步统称 MVP 变换，本课程重点讲解 View 和 Projection 变换

View / Camera transformation

定义相机

Position $\vec{e}$ （摄像机的位置）
Look-at / gaze direction $\hat{g}$（摄像机的朝向，g是单位向量）
Up direction $\hat{t}$（摄像机的上方，垂直于g，$\hat{g}$ 和 $\hat{t}$ 相配合可以确定相机镜头本身的旋转角度）

几个约定俗称的规则：

相机的位置永远在原点
相机永远看向z轴负方向（$-\hat{z}$）
相机的上方永远是y轴正方向（$\hat{y}$）

这里为什么是看向z轴负方向呢？因为我们使用的是右手坐标系，z轴正方向是从屏幕里指向屏幕外，而我们希望相机是看向屏幕里的方向，所以相机看向z轴负方向。

很多图形api或者3d软件使用的是左手坐标系，这时相机看向z轴正方向。

左手坐标系有个坏处，x叉乘y等于-z，这会让人很迷惑，本课程使用右手坐标系。

把相机从当前位置移动到原点，并且让它看向z轴负方向，这个过程叫做 View / Camera transformation

\[ M_{\mathrm{view}} = R_{\mathrm{view}}\,T_{\mathrm{view}} \]

其中 $ R_{\mathrm{view}} $ 是旋转矩阵，$ T_{\mathrm{view}} $ 是平移矩阵。

平移矩阵：把相机从位置 $\vec{e}=(x_e,y_e,z_e)$ 移动到原点

\[ T_{\mathrm{view}} = \begin{bmatrix} 1 & 0 & 0 & -x_e \\ 0 & 1 & 0 & -y_e \\ 0 & 0 & 1 & -z_e \\ 0 & 0 & 0 & 1 \end{bmatrix} \]

旋转矩阵：把相机的朝向 $\hat{g}$ 变换到 $-\hat{z}$ 方向，把 $\hat{t}$ 变换到 $\hat{y}$ 方向，把 $\hat{r}=\hat{g}\times\hat{t}$ 变换到 $\hat{x}$ 方向

这个旋转矩阵不太好求，它的逆矩阵很容易写出来，可以先求它的逆矩阵 $ R_{\mathrm{view}}^{-1} $，然后再对它求逆

\[ R_{\mathrm{view}}^{-1} = \begin{bmatrix} x_{\hat{g}\times\hat{t}} & x_{\hat{t}} & x_{-\hat{g}} & 0 \\ y_{\hat{g}\times\hat{t}} & y_{\hat{t}} & y_{-\hat{g}} & 0 \\ z_{\hat{g}\times\hat{t}} & z_{\hat{t}} & z_{-\hat{g}} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \]

由于旋转矩阵是正交矩阵，所以直接转置后就能得到逆矩阵

\[ R_{\mathrm{view}} = \begin{bmatrix} x_{\hat{g}\times\hat{t}} & y_{\hat{g}\times\hat{t}} & z_{\hat{g}\times\hat{t}} & 0 \\ x_{\hat{t}} & y_{\hat{t}} & z_{\hat{t}} & 0 \\ x_{-\hat{g}} & y_{-\hat{g}} & z_{-\hat{g}} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \]

这个过程也叫 Model / View transformation，因为相机和物体之间的关系不能变，场景中所有的物体也要做这个变换。

Projection transformation

Orthographic (正交) projection
Perspective (透视) projection

正交投影和透视投影的区别：

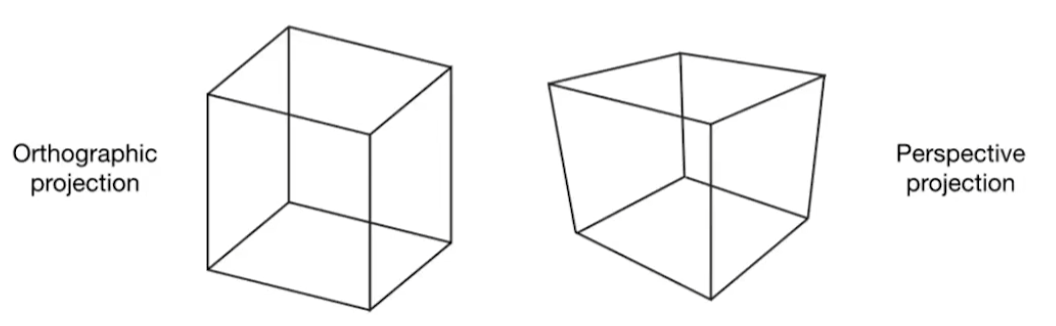
/img/games101-notes/orthographic-perspective-1.png

对正交投影来说，无论摄像机离得有多远，投影的物体大小都不会变：

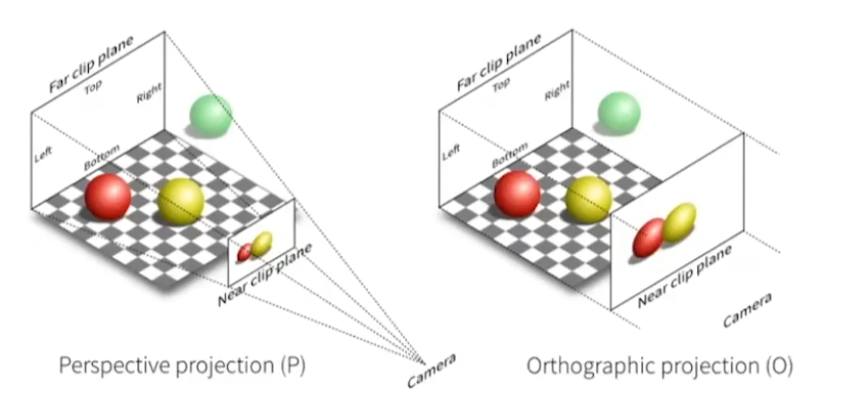
/img/games101-notes/orthographic-perspective-2.png

正交投影 (Orthographic projection)

先做View/Camera transformation，把场景放到摄像机前面
丢掉z坐标
将结果矩形缩放到$[-1,1]$范围内

一般来讲，正交投影是要把任意一个立方体变换为一个正则、规范、标准的（Canonical）立方体（$[-1,1]^3$）, 先做平移变换，然后缩放变换

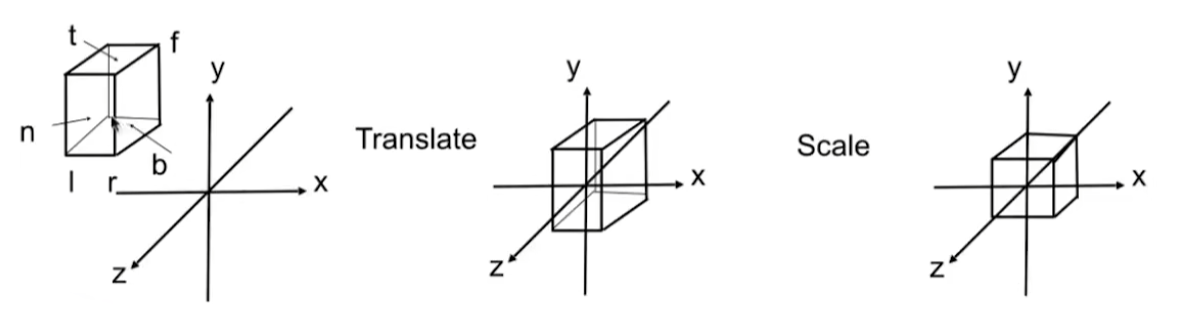
/img/games101-notes/orthographic-projection.png

假设我们要把一个立方体 $[l,r]\times[b,t]\times[n,f]$ 变换为 $[-1,1]^3$，其中 $l$ 是 left，$r$ 是 right，$b$ 是 bottom，$t$ 是 top，$n$ 是 near，$f$ 是 far

变换矩阵为（注意，这里 n 和 f 都是负值，因为相机是看向-z轴的）：

\[ M_{\mathrm{ortho}} = \begin{bmatrix} \frac{2}{r-l} & 0 & 0 & 0 \\ 0 & \frac{2}{t-b} & 0 & 0 \\ 0 & 0 & \frac{2}{n-f} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 & -\frac{r+l}{2} \\ 0 & 1 & 0 & -\frac{t+b}{2} \\ 0 & 0 & 1 & -\frac{n+f}{2} \\ 0 & 0 & 0 & 1 \end{bmatrix} \]

透视投影 (Perspective projection)

透视投影中，相机在原点，相机和视角围成一个四棱锥体（Frustum），相机前面有两个平面，近景平面和远景平面，近景平面和远景平面分别截出这个四棱锥体的顶部和底部。

透视投影分为两步：

先把四棱锥体（Frustum）挤压成一个立方体（Cuboid），对应的变化写作 $M_{\mathrm{persp}\to\mathrm{ortho}}$
然后对这个立方体做一次正交投影 $M_{\mathrm{ortho}}$

最终，完整的透视投影为 $M_{\mathrm{persp}} = M_{\mathrm{ortho}}\,M_{\mathrm{persp}\to\mathrm{ortho}}$

下图是透视投影挤压过程的示意图，其中，$n$ 和 $f$ 分别表示近景平面和远景平面的 z 坐标

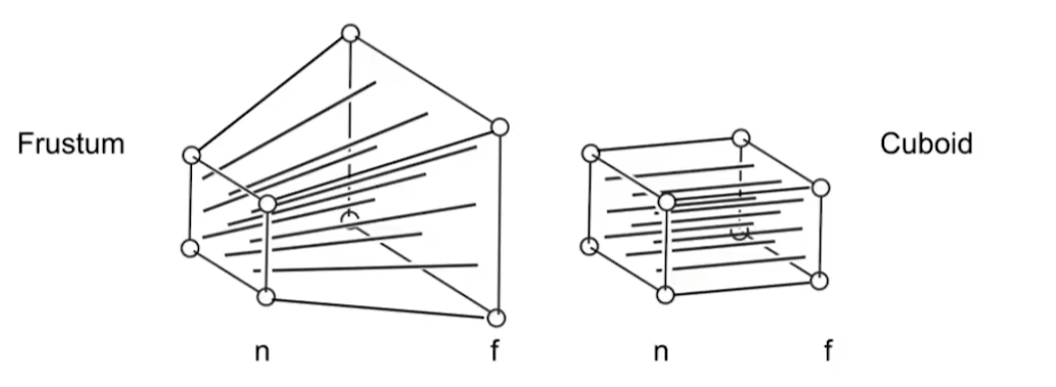
挤压过程中，近景平面的点不变，远景平面的点 z 坐标不变，尺寸变为和近景平面一样的大小。

四棱锥远景平面和近景平面的 y 坐标呈现这样的关系（x 坐标同理）：

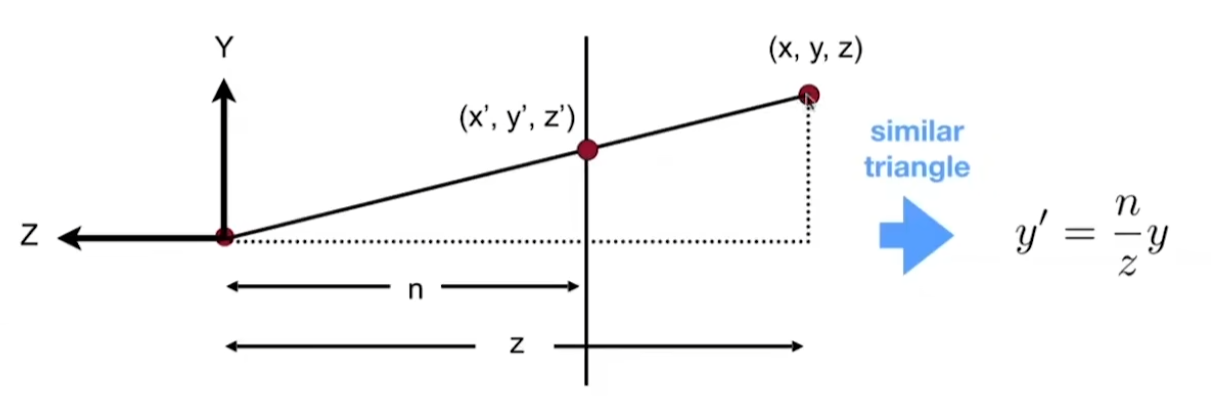
经过一顿推导，得到挤压矩阵（利用了齐次坐标同时乘以一个数坐标不变的性质）：

\[ M_{\mathrm{persp}\to\mathrm{ortho}} = \begin{pmatrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & n+f & -nf \\ 0 & 0 & 1 & 0 \end{pmatrix} \]

Frustum这个四棱锥体又叫视锥，由垂直方向的Fov（Field of View，视野角度）和宽高比（Aspect Ratio）决定，用FovY表示垂直方向的Fov。

用 $[l,r]\times[b,t]$ 来表示近景平面，$n$ 和 $f$ 仍然表示近景平面和远景平面的 z 坐标，那么FovY 和 aspect 与 $l,r,b,t,n,f$ 的关系为：

\[ \tan\!\left(\frac{\mathrm{FovY}}{2}\right) = \frac{t}{\lvert n\rvert} \]

\[ \mathrm{aspect} = \frac{r}{t} \]

注意，投影变换完成后，要对齐次坐标做透视除法（Perspective Divide），即把 $(x,y,z,w)$ 变换为 $(x/w,y/w,z/w,1)$，这样才能得到正确的归一化设备坐标（NDC），而这个过程是非线性的。

光栅化

raster（光栅）这个词来源于德语，就是指屏幕

rasterize（光栅化）是将图像绘制到屏幕上

视口变换（Viewport Transformation）：标准立方体坐标->屏幕坐标

先忽略z坐标，把标准立方体 $[-1,1]^3$ 投影到二维平面上，得到一个正方形 $[-1,1]^2$，然后把这个正方形缩放到屏幕大小 $[0,w]\times[0,h]$ 上，得到一个视口（Viewport）变换矩阵：

\[ M_{\mathrm{viewport}} = \begin{pmatrix} \frac{\mathrm{width}}{2} & 0 & 0 & \frac{\mathrm{width}}{2} \\ 0 & \frac{\mathrm{height}}{2} & 0 & \frac{\mathrm{height}}{2} \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \]

光栅化：把多边形绘制到屏幕上，并填满像素

上面的视口变换只是把标准立方体的坐标变换为屏幕坐标，这些坐标只能构成一个个多边形，但要绘制到屏幕上，还需要把这些多边形填满像素，这个过程叫做光栅化（Rasterization）

三角形

最基础的多边形，它有以下优点：

三角形必然是一个平面，不可能是弯曲的。
三角形内外定义非常清晰，用叉积很容易判断。
容易进行插值计算。

采样（Sampling）

为什么要采样，因为输入数据是一个个坐标，它们围成的多边形是连续的面，而屏幕是由一个个像素组成的，光栅化的过程是要把连续的面离散化到一个个像素上，因此这个过程就叫做采样，屏幕的分辨率就是采样率。

下图是一个采样的例子，判断每个像素的中心是否在三角形内，这里要注意，像素的坐标是以像素的左下角为准，而采样是以像素的中心为准。

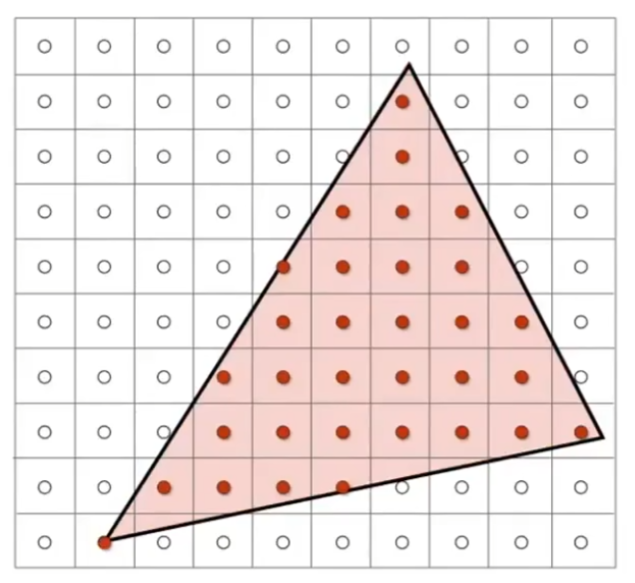
Bounding Box（边界框）是指包含三角形的最小矩形，可以用来加速采样过程。意思是，只对边界框内的像素做采样，边界框外的像素不做采样。

判断像素是否在三角形内部这个过程也叫覆盖测试（Coverage Test）。

直线的采样和绘制可以参考（Bresenham直线绘制算法，代码可参考https://stackoverflow.com/a/16405254）

抗锯齿/反走样（Anti-aliasing）

采样错误是发生在给像素填色这个过程中，总有一些像素位于三角形的边缘，如果我们不做任何额外处理，这些像素要么填色，要么不填色，这就会造成锯齿现象。

采样错误（Sampling Error）

锯齿(Jaggies)

摩尔纹（Moire Patterns），跳过奇数行和奇数列形成

车轮效应（Wagon-wheel Effect），这是一种时间采样错误，一个旋转的车轮看起来像是静止的，或者是反向旋转的。

采样错误的原因基本上是信号变化太快，采样速度跟不上信号变化的速度。

模糊：一种抗锯齿方法

Bluring（Pre-filtering）before sampling，即采样之前先做模糊处理

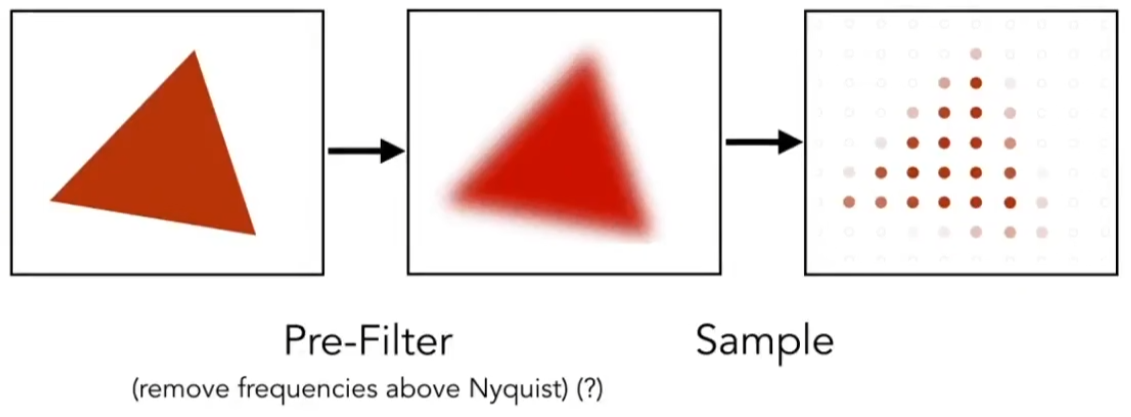
如果把模糊和采样的顺序反过来，先采样，再模糊（Blurred aliasing），效果并不好。

为什么会走样/失真

走样（Aliasing）是因为采样频率远低于信号频率，造成采样结果失真。

滤波

滤波（Filtering）是指丢掉某些特定频率。

傅里叶变换是做从时域（Spatial domain）到频域（Frequency domain）的转换，将一个时域函数拆分成多个不同频率的正弦函数：

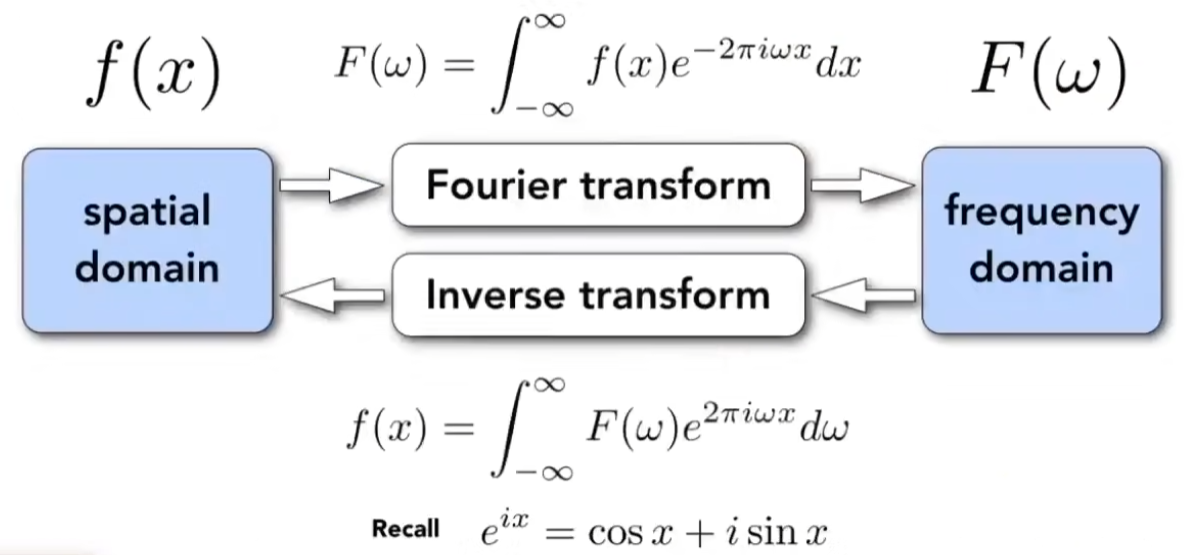
一副图像也可以表示为频谱的形式，频谱中的高频部分对应的是图像中变化剧烈的部分，比如图像内容的边界。

将低频部分过滤掉，保留高频部分，可以得到图像的边界信息，这叫高通滤波。

如果将高频部分过滤掉，保留低频部分，可以得到一副模糊的图像，这叫低通滤波。

怎么滤波

Filtering = Convolution（卷积） = Averaging

（这里的卷积是指时域上的卷积）

一个简单的卷积运算示例，filter相当于一个滑动窗口，从左向右移动，每滑动一次，就将signal和filter做一次点积操作，得到一个新的信号，这其实是一个求原始信号加权平均的操作：

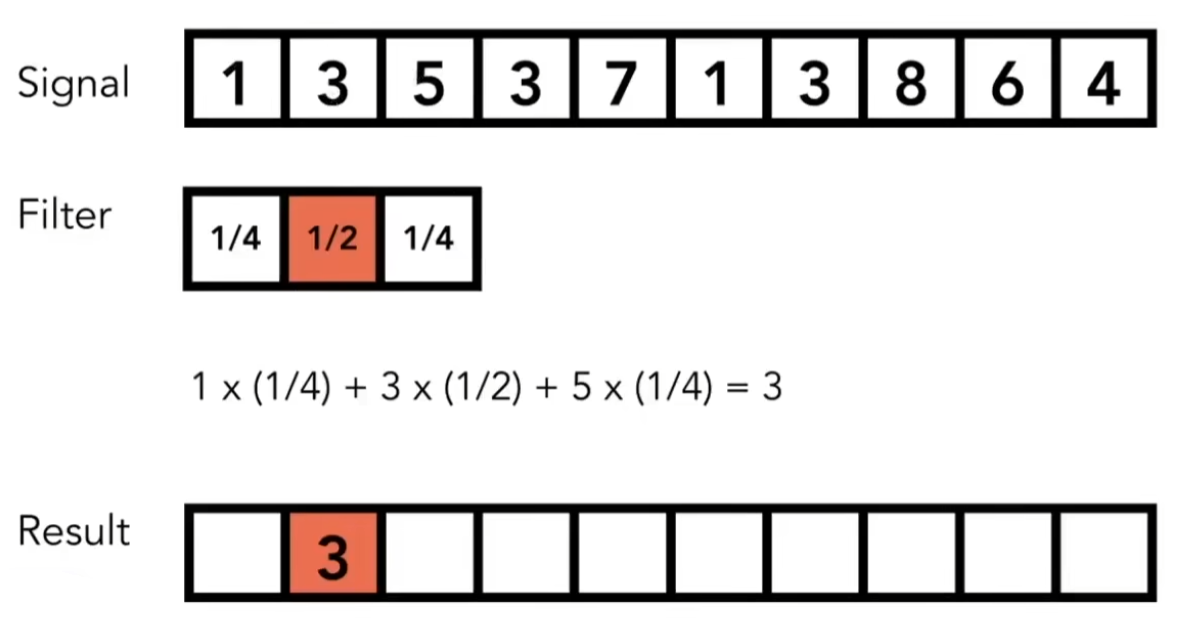
时域上的卷积等于频域上的乘积，时域上的乘积等于频域上的卷积。

下面是一个对图像做卷积的例子，对3x3的区域做卷积，相当于对这块区域做了一个加权平均，起到了模糊的效果，这也相当于对图像做了一个低通滤波：

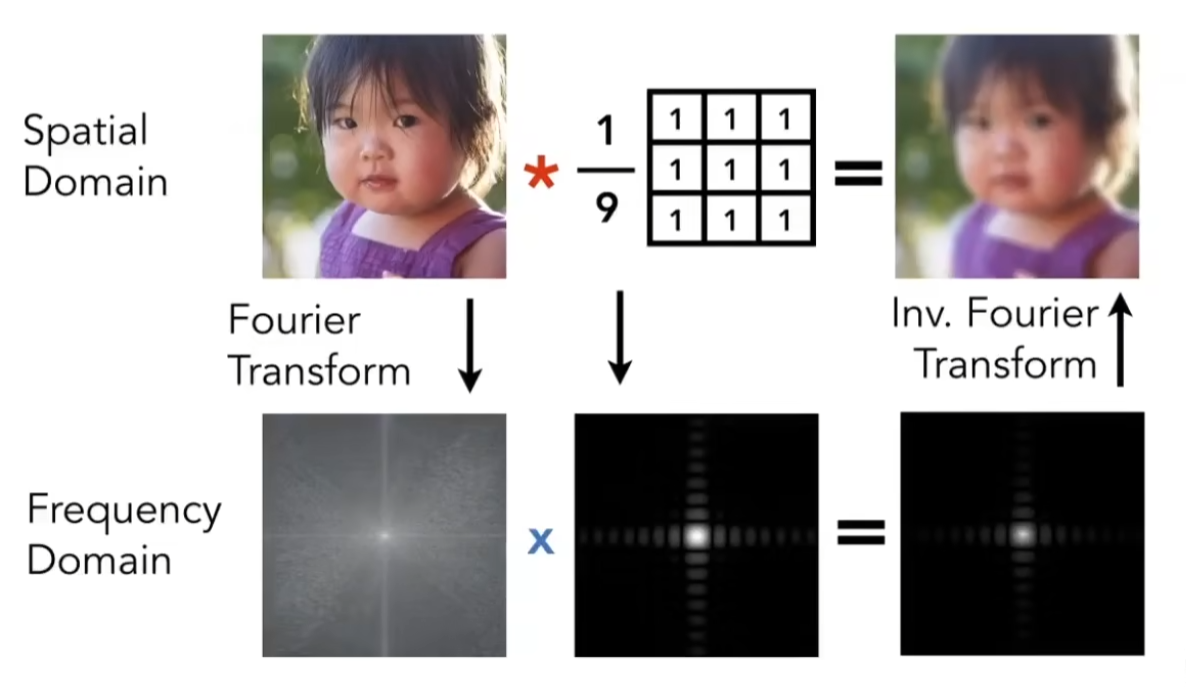
（卷积的简单介绍）

上面提到的Filter，中文有很多种叫法：“核”、“滤波器核”、“卷积核”、“卷积模板”。

对图像所做的滑动点积操作，数学上称为互相关运算，如果先将卷积模板旋转180度，然后再做互相关运算，才叫卷积运算，也就是说，数学上的卷积运算 = 卷积模板旋转180度 + 互相关运算。

从信号的角度分析采样和走样

采样是在时域上将原始信号和冲激序列函数相乘，在频域上是将原始信号的频谱和冲激序列函数的频谱做卷积。

采样在频域上其实是重复一个原始信号的频谱。

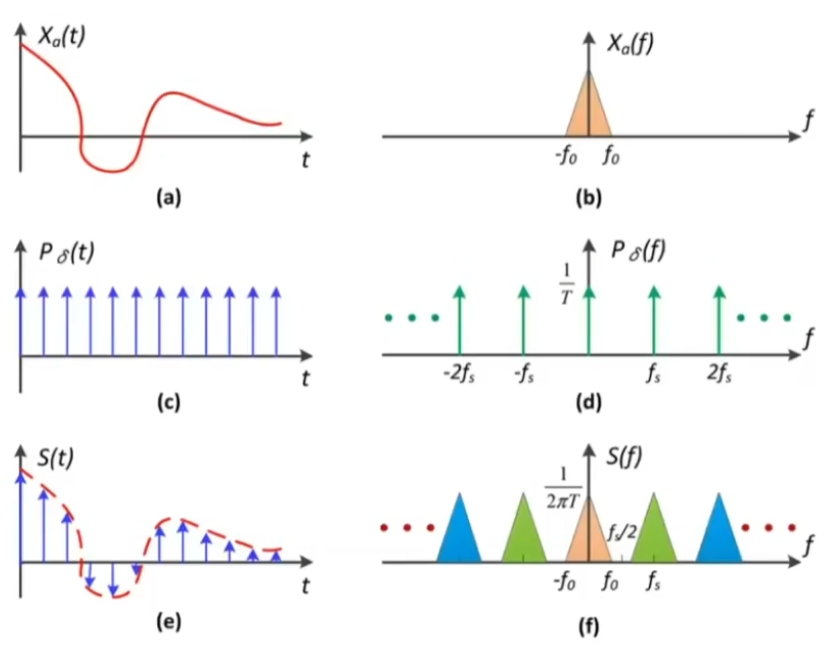
走样实际上是在采样后，频域上的原始频谱发生了混叠（采样频率越低，冲激序列的频谱越在低频集中）

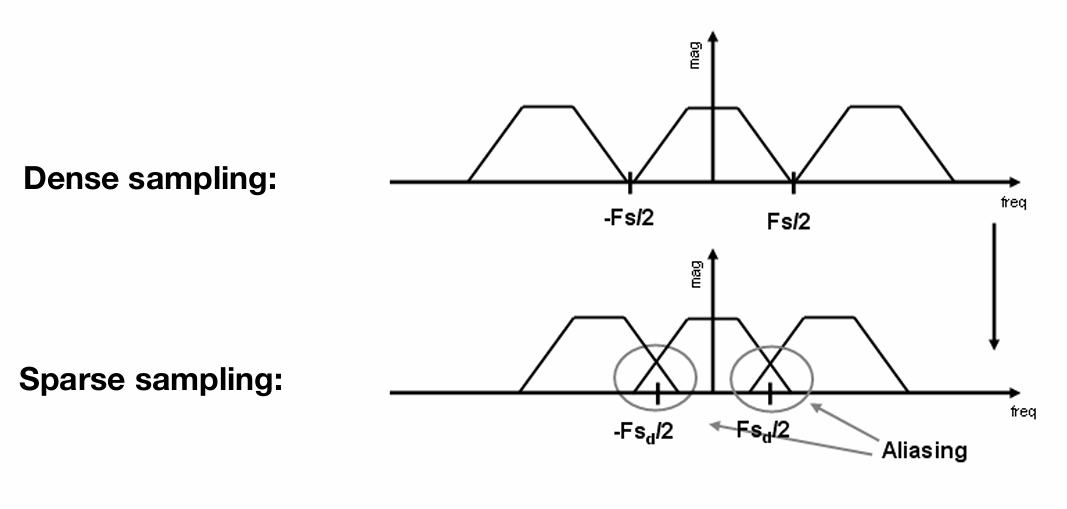
（奈奎斯特采样定理这里没讲）

如何降低采样错误

提升采样率
反走样，例如前面提到的，先做模糊，再采样

通过模糊实现抗锯齿

用一个像素大小的滤波器（Box-blur filter）对三角形做卷积操作，对三角形边缘的颜色做加权平均，将其模糊化。

然后在每个像素中心点位置做采样。

滤波器的权重按照像素覆盖三角形的面积比例来定。

多重采样抗锯齿（MSAA, Multi-Sample Anti-Aliasing）

计算单个像素被三角形覆盖的比例这个过程比较复杂，有一个近似方法，就是把单个像素划分为多个采样点（例如2x2、4x4），用多个采样点采样来近似这个比例，最后根据比例为像素填色。

模糊操作同时也完成了采样这一过程。

MSAA的代价是计算量增大，因为采样点增多了。

MASS的黑边问题，因为有些像素被三角形覆盖的比例很小，这些像素的颜色会很暗，形成黑边，有两个解决办法：

为覆盖率指定一个阈值，只有高于这个阈值的像素才填色，这样，最暗的像素的亮度一定不会低于这个阈值。它的问题在于：（1）MASS的效果会变差，因为有些像素本来是有颜色的，但由于覆盖率低于阈值而被丢弃了；
将覆盖率过低的像素的深度值设置为无穷远，这样，这些像素可以被后绘制的三角形覆盖掉，它解决了方案1的问题。

其他抗锯齿方法

FXAA(Fast Approximate Anti-Aliasing)
不是增加采样点，而是通过对渲染图像的后处理，把图像上的锯齿边界找到，然后去掉锯齿，换成平滑的边界（简单来说就是把锯齿P掉）。
TAA(Temporal Anti-Aliasing)
利用时间做抗锯齿，利用前一帧的采样信息来辅助当前帧的采样，具体来说，就是把MSAA划分出来的多个采样点，放在时间尺度上去处理。
超分（Super Resolution）/超采样（Super Sampling）
- 用低分辨率渲染图像，然后用AI算法把图像放大到高分辨率。
- DLSS（Deep Learning Super Sampling）

总结

抗锯齿本质上是对像素颜色的调整，目的是让图像看起来更平滑，并不涉及坐标的处理。

滤波方法是要将图像模糊化，降低图像的高频部分，而图像的频率是由图像的亮度（灰度）变换决定的，从这个角度来看，抗锯齿也仅仅是对图像颜色的处理。

物体可见性

画家算法（Painter's Algorithm），从远道近画，近处的物体覆盖远处的物体。

画家算法的问题是很多情况很难说清楚哪个物体在前，哪个物体在后，例如两个三角形相交的情况。

Z-Buffer

深度缓存（Depth Buffer），也叫z-buffer，给每个像素增加一个深度值，用z-buffer记录当前已绘制像素的深度值，新绘制的像素如果深度值更小，就覆盖当前像素，否则丢弃。

利用深度缓存判断物体遮挡这个过程也叫深度测试（Depth Testing）。

主要流程：

先把深度缓存初始化为无限远
对每个三角形做光栅化
对每个像素做采样
计算采样点的深度值
如果深度值小于当前像素的深度值，就更新像素颜色和深度值，否则丢弃

这里没讲多个三角形深度相同的情况如何处理。

透视投影深度矫正

在深度测试时，不能直接用透视投影后的z坐标做深度值，因为对于透视投影来说，挤压视锥体的过程会改变z坐标的线性关系，如果直接用透视投影变换后的z坐标做深度值，会导致深度测试错误。

因此，我们需要对z坐标做矫正，一般采用以下公式：

\[ Z = \frac{1}{\dfrac{\alpha}{w_0} + \dfrac{\beta}{w_1} + \dfrac{\gamma}{w_2}} \]

\[ z_p = \left(\frac{\alpha z_0}{w_0} + \frac{\beta z_1}{w_1} + \frac{\gamma z_2}{w_2}\right) Z \]

其中，$0,1,2$ 分别代表三角形的三个顶点，$w_0,w_1,w_2$ 是三角形顶点的齐次坐标，$\alpha,\beta,\gamma$ 是重心坐标。

这里利用到一个性质，经过投影变换后，点的齐次坐标 $w$ 的值刚好等于变换前的 z 坐标的值（即在视图空间下的z值）。

插值

由于我们只知道三角形顶点的深度值，如何计算三角形内部任意一点的深度值呢？这就需要插值。

可以使用重心坐标插值（Barycentric Coordinates Interpolation）

对屏幕空间三角形 ABC 内任意点 P，用三个权重 α, β, γ 表示
- P = αA + βB + γC，且 α + β + γ = 1
- α, β, γ 分别等于子三角形 PBC、PCA、PAB 的面积占比（带符号面积）
这些权重有两个核心用途：
- 覆盖测试：若 α, β, γ 全同号（通常 ≥ 0），P 在三角形内或边上。
- 属性插值（颜色、深度、法线、UV 等）：attr(P) = α·attr(A) + β·attr(B) + γ·attr(C)。
深度插值
得到 α, β, γ 后，可以求z插值，这里$A_w$、$B_w$、$C_w$都是齐次坐标：

\[ z_{\text{插值}} = \frac{\alpha \frac{A_z}{A_w} + \beta \frac{B_z}{B_w} + \gamma \frac{C_z}{C_w}} {\alpha \frac{1}{A_w} + \beta \frac{1}{B_w} + \gamma \frac{1}{C_w}} \]