games101 二、着色

着色（Shading）

根据不同材质和光照条件，绘制物体的颜色，这个过程叫着色（Shading）。

着色是作用于一个个着色点（shading point）的。

Blinn-Phong 反射模型（Blinn-Phong Reflectance Model）

1. Specular highlight（镜面高光）
2. Diffuse reflection（漫反射）
3. Ambient reflection（环境光反射）

shading定义

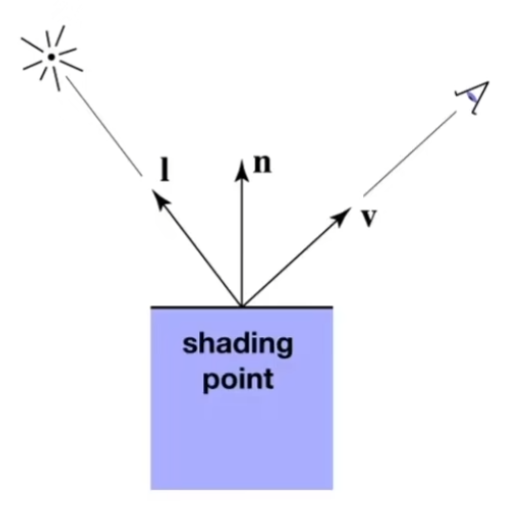
• Viewer direction \(\vec{v}\)，观察者方向向量
• Surface normal \(\vec{n}\)，表面法线向量
• Light direction \(\vec{l}\)，光源方向向量
• Surface parameters，表面材质参数
• color
• Shininess

上面这些向量都是单位向量。

Shading考虑的是，在不同的光照和表面材质的作用下，表面上每个点的颜色是怎样的。

Shading只考虑一个物体自己和光线的交互，不考虑物体之间的相互影响，如阴影（Shadow）、反射（Reflection）等。

法线变换

我们已经知道，顶点位置需要经过MV变换后，再做反射计算，那么自然，法线也需要经过变换后才能参与反射计算。

但是法线不能直接用MV矩阵变换，因为法线是垂直于表面的向量，直接用MV矩阵变换后，可能不再垂直于表面。

为了保证法线变换后仍然垂直于表面，我们需要用MV矩阵的逆转置矩阵（Inverse Transpose Matrix）来变换法线。

逆转置矩阵，即：

\[(M^{-1})^T\]

漫反射（Diffuse Reflection）

漫反射模拟光线照射到粗糙表面上的效果。

漫反射的入射光线会均匀地向各个方向反射。

考虑光线接收

Lambert的余弦定律（Lambert's Cosine Law）：

假设入射光线是平行的，物体表面的法线和入射光线夹角越大，单位表面接收到的光就越少，用 \(\theta\) 表示入射光线和法线的夹角，\(cos\theta=\vec{l} \cdot \vec{n}\)。

考虑光线发射

有一个点光源，我们可以以光源为中心，画出多个半径不同的球面，同一个球面上每个点的光照强度相同，不同球面的总光照强度相同，因此球面上的单个点的光照强度与距离光源的距离有关，距离越远强度越低。

定义 \(I\) 为半径为1的球面上某一点的光照强度（Intensity），球面总光照强度为 \(4\pi I\)，那么距离光源 \(r\) 处的一点上光照强度为 \(I/r^2\)。

漫反射公式

由此可得一个shading point上的漫反射公式：

\[L_d = k_d \frac{I}{r^2} \max(0, \vec{l} \cdot \vec{n})\]

其中，\(k_d\) 为漫反射系数 （Diffuse coefficient），为1时表示完全反射，亮度最亮，为0时表示完全吸收，亮度最暗，当它为向量时，表示的就是颜色系数。

由于漫反射均匀地向各个方向反射，所以不管从哪个方向观测，看到的颜色都是一样的。

高光（Specular Highlight）

只有当观察方向和镜面反射方向接近时，才会看到高光，因此光照强度（Intensity）与观察方向有关。

观察方向和镜面反射方向接近也也意味着半程向量 \(\vec{h}\) 和法线方向接近，半程向量是指光线入射方向和观察方向的角平分线方向。

\[\vec{h} = \frac{\vec{l} + \vec{v}}{|\vec{l} + \vec{v}|}\]

高光的反射公式为：

\[L_s = k_s \frac{I}{r^2} \max(0, \vec{h} \cdot \vec{n})^{p}\]

其中，\(\vec{h} \cdot \vec{n}\) 为 半程向量和法线的夹角余弦 \(\cos{\alpha}\)，\(k_s\) 为高光系数（Specular coefficient），\(p\) 是为了加快 \(\cos{\alpha}\) 的衰减，\(p\) 的值较大时，夹角 \(\alpha\) 稍微大一点，\(\cos{\alpha}\) 的值就会降低很多，高光就会衰减很快，体现在视觉上就是高光比较集中。

Blinn-Phong 模型将光线接收项 \(\vec{l} \cdot \vec{n}\) 简化掉了。

环境光（Ambient Light）

环境光来自四面八方，我们假任何一个点接收到的环境光永远相同。

\[L_a = k_a I_a\]

\(I_a\) 为环境光强度（Ambient Intensity），是一个恒定值，\(k_a\) 为环境光系数（Ambient coefficient）。

合起来

将三种光照模型合起来：

\[L = L_a + L_d + L_s\]

着色频率（Shading Frequency）

着色频率研究的是如何让渲染结果更精细，更平滑，比如，一个球体实际上是由很多三角形组成的，如果每个三角形只计算一个着色点，那么渲染出来的球体就会有棱角，为了解决这个问题，我们可以增加着色点的数量，比如在每个三角形内部进行插值计算，以提高着色频率，这样就能让渲染结果更平滑。

注意下面的方法提到了计算顶点法线，实际上，有些模型格式，例如obj格式，已经包含了顶点法线数据。

Flat Shading (Face)

一个三角形面只有一个法线，把三角形面视为一个平坦的平面。

Gouraud Shading (Vertex)

求出几个顶点的法线，计算出顶点的颜色，然后在三角形面内进行颜色插值。

Phong Shading (Pixel)

注意这个并不是Blinn-Phong反射模型。

求出几个顶点的法线，在三角形面内进行法线插值，然后计算出每个像素点的颜色。

题外话（一点思考）

使用顶点法线插值，不会改变几何，只是光照时让几何体表面显得更平滑。

这叫做法线平滑（Normal Smoothing）。

如果我有个比较复杂的几何体，我希望它某一部分的渲染使用面法线，让他的棱角更分明，而其他部分使用顶点法线插值，让他的表面更圆滑，图形学上有这种技术吗？或者说，这对于图形学来说，是个问题吗？

gpt告诉我:

有，并且非常常见。这不是问题，而是标准做法。

可用的技术与做法：

硬边/平滑组（Smoothing Groups）/法线拆分（Normal Split）：在硬边处“拆分顶点”，给该边两侧三角形的顶点写入各自的面法线；其余区域用平滑顶点法线。大多数DCC/引擎支持（OBJ/FBX可存“面-顶点法线”）。 按角度阈值生成法线：导入时按夹角>阈值就断边，用面法线；否则合并求平均法线。 着色器里混合：在片元着色器同时拿到“插值法线”（平滑）和“几何面法线”，用掩码（顶点属性或纹理）选择或混合二者。

示例（GLSL 片元，世界或视空间一致）：

// ...插值进来的数据...
in vec3 vPosWS;         // 片元位置(世界/视空间)
in vec3 vNormalWS;      // 插值后的平滑法线
in vec2 vUV;            // 可选，用于区域掩码
uniform sampler2D uMask; // R=1 用面法线，R=0 用平滑
// ...existing code...
void main() {
    vec3 N_smooth = normalize(vNormalWS);
    vec3 N_flat   = normalize(cross(dFdx(vPosWS), dFdy(vPosWS))); // 面法线
    float w = texture(uMask, vUV).r; // 或者用顶点属性/材质开关
    vec3 N = normalize(mix(N_smooth, N_flat, w));
    // 用 N 做后续光照
}

其他要点：

• 用 flat 插值限定符也可让某个 varying 按“每面”传值，但要保证三顶点携带相同数据或用几何着色器/顶点复制。
• 硬边会增加顶点数；若用 dFdx/dFdy 求面法线，请确保用同一空间的 vPos，并注意导数在分支/多采样处的连续性。
• 若用法线贴图，平滑区应保持一致的切线空间（常用 MikkTSpace）。

结论：同一几何体中混合“面法线的硬朗”和“顶点法线的圆滑”是行业常规工作流，直接用硬边/平滑组或着色器掩码即可实现。

以上全部都是gpt告诉我的。

如何计算顶点的法线？

对顶点所在面的法线进行平均。

\[ \vec{n}_v = \frac{\sum_{i=1}^{k} \vec{n}_i}{|\sum_{i=1}^{k} \vec{n}_i|} \]

如何对法线插值？

Barycentric coordinates interpolation（重心坐标插值）

实时渲染管线（Real-time Rendering Pipeline）

1. Vertex Processing，将顶点从模型空间变换到屏幕空间（MVP变换）
2. Triangle Processing，将顶点划分为一个个三角形
3. Rasterization，光栅化，将三角形离散化为一个个采样点（Fragments），抗锯齿
4. Fragment Processing，根据采样结果对每个像素进行着色，深度测试 / 可见性测试
5. Framebuffer Operations

着色（Shading）主要发生在Vertex Processing 和 Fragment Processing，控制着色的程序叫做 Shader。

图形管线运行在GPU上，充分利用GPU的并行计算能力。

Shader

Shader 需要用硬件上执行的语言来编写，比如 GLSL、HLSL 等。

Shader 只需要关心单个顶点或像素的着色，不需要写循环等控制结构。

Shader 分为两种：

• Vertex Shader，顶点着色器
• Fragment Shader，片段着色器/像素着色器

纹理映射（Texture Mapping）

纹理是对表面上的每个点赋予一个属性。

纹理映射是把一张二维的图片映射到三维物体表面上的过程，物体表面的每一个顶点都要对应纹理上的一个点。

纹理上的坐标系通常称为uv坐标系，u表示水平方向，v表示垂直方向。

Tilable texture（可平铺纹理），纹理在上下左右方向上重复使用的时候，起到一种无缝衔接的效果。

纹理映射只规定了三维顶点和二维纹理坐标之间的映射关系，而对三角形面内的某一点来说，它的纹理坐标需要通过重心坐标插值来计算。

重心坐标插值（Barycentric Coordinates Interpolation）

重心坐标插值可以用来做纹理坐标插值，法线插值，颜色插值等。

重心坐标的计算方法如下：

对于一个三角形 \(\triangle ABC\)，以及三角形内的一个点 \(P\)，我们可以将 \(P\) 表示为 \(A\)，\(B\)，\(C\) 的线性组合：

\[P = \alpha A + \beta B + \gamma C\]

其中，\(\alpha + \beta + \gamma = 1\)，且 \(\alpha, \beta, \gamma \geq 0\)。

由 \(\alpha\)、 \(\beta\)、\(\gamma\) 这三个系数构成的向量 \((\alpha, \beta, \gamma)\) 就是点 \(P\) 的重心坐标。

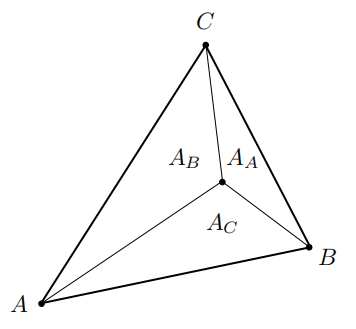
\(\alpha\)、 \(\beta\)、\(\gamma\) 可以通过以下方法求出（\(A\) 代表面积）：

\[\alpha = \frac{A_A}{A_{ABC}}, \quad \beta = \frac{A_B}{A_{ABC}}, \quad \gamma = \frac{A_C}{A_{ABC}}\]

三角形的重心坐标为 \((\frac{1}{3}, \frac{1}{3}, \frac{1}{3})\)，即，三角形的重心刚好将三角形分成三个等面积的小三角形。

假设点 \(P\) 的坐标为 \((x,y)\)，下面是计算 \(\alpha\)、 \(\beta\)、\(\gamma\) 的公式（利用叉乘就可以推导出）：

\[ \alpha = \frac{-(x - x_B)(y_C - y_B) + (y - y_B)(x_C - x_B)} {-(x_A - x_B)(y_C - y_B) + (y_A - y_B)(x_C - x_B)} \]

\[ \beta = \frac{-(x - x_C)(y_A - y_C) + (y - y_C)(x_A - x_C)} {-(x_B - x_C)(y_A - y_C) + (y_B - y_C)(x_A - x_C)} \]

\[ \gamma = 1 - \alpha - \beta \]

对于任意向量的插值，也是一样的：

\[V_P = \alpha V_A + \beta V_B + \gamma V_C\]

由于在投影变换过程中，三角形会被拉伸变换，点的重心坐标会变，所以什么时候做插值，要区分清楚。

应用纹理

1. 光栅化后，对屏幕上的每一个采样点进行纹理坐标插值，得到对应的纹理坐标（\(u,v\)），\(u,v\) 坐标的值通常在0~1之间。
2. 着色时，将纹理图片上的颜色作为漫反射系数 \(k_d\)。

纹理反走样

纹理放大（Texture Magnification）和纹理缩小（Texture Minification）

纹理太大或太小，有可能发生在场景有一定深度时，近处的物体需要用大纹理，远处的物体需要用小纹理。

texture太小怎么办？

纹理图像中的一个像素叫做texel，纹理放大时需要对texel进行插值。

插值解决的是，给定一个非整数的纹理坐标，如何计算出对应的颜色。

Bilinear Interpolation（双线性插值）

如果是线性插值，很简单，比如我们想在 \(\vec{v_0}\) 和 \(\vec{v_1}\) 之间插值，插值系数为 \(x\)，那么插值结果为：

\[ lerp(x, \vec{v_0}, \vec{v_1}) = \vec{v_0} + x(\vec{v_1} - \vec{v_0})\]

双线性插值是在二维平面上的四个点构成的矩形区域内进行插值，实际上就是做三次线性插值，先在水平方向上做两次线性插值，然后在垂直方向上做一次线性插值。

texture太大怎么办？

texture太大，要把它映射到一个小的区域上，这个过程实际上是对纹理降低采样率采样，和覆盖测试类似，同样会出现走样问题（摩尔纹，锯齿等）。

从现象上看，出现走样是因为一个像素（即一个采样点）对应了一大块纹理区域。

解决方法: 1. 增加采样点 2. 不做采样，给定一个纹理区域，立刻得到这个区域的平均值

这实际上是两个理念的区别，Point Query 和 Range Query。

Mipmap

Mipmap可以用来做正方形范围查询（Range Query）

Mipmap的原理是这样的，在渲染之前预先生成一系列不同分辨率的纹理图像，然后在渲染时根据需要选择合适分辨率的纹理图像进行采样。

我们把每个分辨率的图像称为1层，用 D 表示，D0 层为原始图像，D1 层为原始图像宽高各减半后的图像，D2 层为 D1 层宽高各减半后的图像，以此类推，每个层的图像大小为上一层的四分之一。

经过级数求和，可以知道总共需要4/3倍的存储空间，也就是说，Mipmap 仅需要额外的 1/3 存储空间。

如何知道选择哪一层的图像？或者说，如何知道一个像素对应的纹理区域有多大？

选择一个像素相邻的两个像素，计算它们在纹理空间中的距离，距离越大，说明纹理区域越大，选择的层数就越高。

以下公式可以近似计算出像素对应的Mipmap层数D，L代表像素对应的纹理空间的边长，它是取像素分别距离x方向和y方向上的像素在纹理空间中的距离的最大值，其中，\(x\)和\(y\)代表屏幕空间的坐标，\(u\)和\(v\)代表纹理空间的坐标。

\[ D = \log_{2} L \]

\[ L = \max\!\left( \sqrt{\left(\frac{du}{dx}\right)^2 + \left(\frac{dv}{dx}\right)^2}, \sqrt{\left(\frac{du}{dy}\right)^2 + \left(\frac{dv}{dy}\right)^2} \right) \]

举个例子，假如算出来的L是4，意味着，一个像素对应的原始纹理（D0层）区域是4x4的，而D2层的一个像素正好对应原始纹理的4x4区域，因此，我们应该选择D2层的图像进行采样。

如果D不是整数怎么办？比如D=1.8，很简单，使用插值，先在D1层和D2层分别做双线性插值，然后再对结果做线性插值，这叫做三线性插值（Trilinear Interpolation）。

Mipmap的限制

Mipmap只能处理正方形区域的查询，不能处理任意形状的区域查询。

这会导致深度较大的场景中，远处的物体可能会过于模糊。

各向异性过滤（Anisotropic Filtering）

各项异性过滤预先计算出不同长宽比例的纹理图像，然后在渲染时根据需要选择合适的图像进行采样。

这叫Ripmap。

EWA Filtering

EWA Filtering（Elliptical Weighted Average Filtering，椭圆加权平均过滤）可以处理任意形状的区域查询。

它的原理是把一个不规则的纹理区域近似为多个椭圆，需要查询多次，然后对结果进行加权平均。

环境贴图（Environment Mapping）

环境贴图是为了模拟物体表面的反射效果。

它是把不同方向的环境光照信息预先保存到纹理中，然后在渲染时根据物体表面的法线方向，从纹理中采样出对应的环境光照信息，作为物体表面的反射光照。

假设环境光都是来自无限远处，只记录环境光的方向信息。

球面环境贴图（Spherical Environment Mapping）是将环境光照信息映射到一个球面上。

为了解决球面贴图展开为矩形时的扭曲问题，可以使用立方体贴图（Cubemap），将环境光照信息映射到一个立方体的六个面上。

凹凸贴图 / 法线贴图（Bump Mapping / Normal Mapping）

贴图中记录表面上每个点的相对高度信息，在渲染时根据高度调整表面法线，从而模拟出表面的凹凸效果。

如何计算一点 \(P\) 新的法线呢？

假设原始的法线为 \((0,0,1)\)，高度函数为 \(h(u,v)\)，\(u\) 和 \(v\) 是纹理坐标。

先求点 \(P\) 分别在 \(u\) 和 \(v\) 方向的导数，分别在 \(u\) 和 \(v\) 方向上移动一个单位长度，点 \(P\) 的高度分别为 \(h(u+1)-h(u)\) 和 \(h(v+1)-h(v)\)，那么点 \(P\) 在 \(u\) 方向上的导数为，其中，\(c_1\) 和 \(c_2\) 分别是两个固定的系数：

\[ \frac{dp}{du} = c_1 * [h(u+1)-h(u)] \]

\[ \frac{dp}{dv} = c_2 * [h(v+1)-h(v)] \]

根据导数，可以求出切线方向向量，然后可以求出法线方向向量：

\[ \vec{n} = (-dp/du, -dp/dv, 1).normalize() \]

注意这里的法线是局部空间的法线，需要经过逆转置矩阵变换到世界空间。

位移贴图（Displacement Mapping）

位移贴图同样也是为了模拟表面的凹凸效果，不同的是，位移贴图直接改变表面上每个点的位置，而不是改变法线。

位移贴图要求三角形网格足够密集，使得着色时的采样率能够跟得上贴图的顶点变化速度。

directx有一套近似机制，动态曲面细分（Dynamic Tessellation），可以在渲染时动态增加三角形网格的密度，而不需要建模时就建好密集的网格。

纹理的其他应用

• 三维噪声（3D Procedural Noise），是一种三维纹理。
• 环境光遮蔽（Ambient Occlusion），用于模拟环境光照射下在物体表面产生的阴影效果，比如物体表面倒映出屋子里的窗户，只有玻璃是亮的，其他地方是暗的。
• 用于体积渲染（Volume Rendering）的三维纹理（3D Texture）。

阴影贴图（Shadow Mapping）

如何运用光栅化技术来实现阴影效果？

答案是Shadow Mapping（阴影贴图）

• 在计算阴影的过程中，不需要知道场景中的几何信息
• 可能会产生走样问题

要点是只有当light和camera都能看到这个点的时候，我们才认为它不在阴影里，这个很好理解，camera能不能看到这个点决定这个点能不能着色，而light能不能看到这个点决定这个点着什么颜色。

Shadow mapping只能处理点光源。

只能生成硬阴影（Hard Shadow）

• 硬阴影：阴影的轮廓清晰，一个点要么在阴影里，要么不在阴影里
• 软阴影：阴影的轮廓比较模糊

如何实现

第一步，假设光源的位置有个相机，我们先用光源相机渲染一张深度图（Depth Map），深度图中记录的是从光源看到的每个像素点的深度值。

第二步，从真正的相机位置再次看向场景，对于每个像素点，拿到这个像素点对应的几何点，将这个点变换到光源相机空间，计算出这个点的深度值，然后比较这个深度值和深度图中的深度值之间的关系，如果光源和相机都能看到这个点，这个点不在阴影里，否则，这个点在阴影里。

这个方案存在几个问题：

• 深度图是有一个具体的分辨率的，可能会存在走样问题。
• 每个光源都会增加一次渲染过程，提高了计算成本。

软阴影

一个完全看不到光源的地方，叫本影（Umbra），一个部分看得到光源的地方，叫半影（Penumbra）。

这是个自然现象，在自然界中有很多例子，比如日食。

这是由于光源本身有一定大小导致的，如果是点光源，则不存在半影。