games101 四、光线追踪

光线追踪解决什么问题

软阴影（Soft Shadow）
光泽反射（Glossy Reflection）：有一些光泽，但不是完全镜面反射
间接光照（Indirect Illumination）：光线在场景中的多次反射

光栅化快，但是质量低，光线追踪更精确，更符合物理规律，但是慢。

光线（Light Ray）

假设光线沿着直线传播。
假设两个光线不会碰撞，各传播各的。
光线从光源发出，经过场景中的传播和反射，最后到达眼睛。
光路可逆（Reciprocity），假设眼睛发出光线，经过场景中的传播和反射，最后能到达光源。

光线追踪就是利用光路可逆的原理，从眼睛出发，追踪光线在场景中的传播路径，直到光源。

光线投射（Ray Casting）

从眼睛出发，投射光线，找到光线和场景中物体的交点，再从交点出发，投射光线到光源，判断交点是否在阴影中，如果不在阴影中，就计算着色。

生成Eye Ray：每个像素投出一个光线

眼睛和场景之间有一个成像平面（Image Plane），从眼睛发出一个光线（Eye Ray / Camera Ray）穿过成像平面上的一个像素，到达场景中最近的一个物体，找到交点。

像素着色

从交点往光源连一条线（Shadow Ray），根据这条线有没有被物体阻挡，判断这个点在不在阴影里。

再根据法线，光线的入射方向，眼睛的观察方向，计算这个点的颜色。

Recursive (Whitted-Style) Ray Tracing

可以处理光线多次的反射和折射。

由于光线在场景中弹射多次，光线和场景中的物体会有多个交点，每个交点都会跟光源连线，做阴影判断。

光线在场景中每个交点的着色都会叠加到同一个像素上。

如果存在折射，那么光线和物体表面的交点会产生两条新的光路，一条是反射光路，一条是折射光路，这两条光路最终都汇聚回光源。

（从眼睛出发的角度来讲，这是同一条光线的弹射过程，但是，从光源的角度来讲，它其实是发出了多条不同的光线，经过不同的光路，最终汇聚到眼睛。）

光线在弹射的过程中，能量会有衰减。

Primary Ray：从眼睛出发的光线。
Secondary Ray：二次弹射的光线。
Shadow Ray：从交点到光源的光线。

求交点（Ray-Surface Intersection）

光线由起点和方向定义。

光线上的任何一点，都可以用以下公式表示：

\[ \mathbf{r}(t) = \mathbf{o} + t\,\mathbf{d},\quad 0 \le t < \infty \]

其中，\(\mathbf{o}\) 是光线的起点，\(\mathbf{d}\) 是光线的方向，\(t\) 是一个非负实数。

光线与球的求交

球的隐式方程是：

\[ (\mathbf{p}-\mathbf{c})^2 - R^2 = 0 \]

球面上任意一点 \(\mathbf{p}\)，到球心 \(\mathbf{c}\) 的距离等于球的半径 \(R\)。

求交方程：

\[ (\mathbf{o} + t\,\mathbf{d} - \mathbf{c})^2 - R^2 = 0 \]

使用二次方程求根公式，就能解出 \(t\)：

\[ t = \frac{-b \pm \sqrt{b^{2} - 4ac}}{2a} \]

光线和一般隐式表面的求交

隐式表面（Implicit Surface）是指由一个隐式函数定义的曲面：

\[ \mathbf{p} : f(\mathbf{p}) = 0 \]

求交方程：

\[ f(\mathbf{o} + t\,\mathbf{d}) = 0 \]

光线和三角形Mesh的求交

光线和Mesh求交能干嘛：

渲染方面：判断可见性（Visibility），判断阴影（Shadow），光照计算（Lighting）。
几何方面：判断一个点是否在Mesh内部。

判断内外部，有一个简单的方法：从这个点出发，向任意方向发射一条光线，计算光线和Mesh的交点个数，如果是奇数，说明这个点在内部，如果是偶数，说明这个点在外部。

如何计算？

光线和三角形的求交

先计算光线和平面的交点，然后判断交点是否在三角形内。

平面可以定义为一个点 \(p'\) +法线，只要一个点和 \(p'\) 的连线和法线 \(n\) 垂直，就说明这个点在平面上，即

\[ \mathbf{p}: (\mathbf{p} - \mathbf{p}') \cdot \mathbf{n} = 0 \]

将这里的点和向量写成x、y、z的形式，代入光线方程，就能得到常见的平面方程：

\[ ax + by + cz + d = 0 \]

光线和平面的求交过程：

\[ \begin{aligned} &\text{Set } \mathbf{p} = \mathbf{r}(t) \text{ and solve for } t\\ &(\mathbf{p} - \mathbf{p}') \cdot \mathbf{N} = (\mathbf{o} + t\,\mathbf{d} - \mathbf{p}') \cdot \mathbf{N} = 0\\ &t = \frac{(\mathbf{p}' - \mathbf{o}) \cdot \mathbf{N}}{\mathbf{d} \cdot \mathbf{N}},\quad \text{Check: } 0 \le t < \infty \end{aligned} \]

然后再判断交点是否在三角形内。

Moller Trumbore Algorithm

Moller Trumbore 算法是一种高效的光线和三角形求交算法，一下就能求出光线和三角形的交点。

其基本思想是用三角形重心坐标描述交点的位置。

下图展示了 Moller Trumbore 算法的计算过程，\((1-b_1-b_2)\)、\(b_1\)、\(b_2\) 是重心坐标，\(P_0\)、\(P_1\)、\(P_2\) 是三角形的三个顶点。

上图中将求交过程转换为解线性方程组（因为公式中的向量和点都是三维的），利用克拉默法则（Cramer's Rule）求解，克拉默法则可以用来解n个式子和n个变量的线性方程组。

得到解以后，只要t和三个重心坐标都是非负的，并且重心坐标之和为1，就说明交点在三角形内。

包围盒（Bounding Volume）

最简单的想法是，遍历所有三角形，计算光线和每个三角形的交点，找到最近的交点，但是这个方法很慢。

如何加速计算呢？

包围盒（Bounding Volume）是一个简单的几何体，能包住复杂的几何体。

包围盒的基本思想是：如果光线和包围盒相交，那么光线一定和包围盒内部的某个物体相交；如果光线和包围盒不相交，那么光线一定和包围盒内部的物体不相交。

长方体是最常用的包围盒，我们通常使用轴对齐包围盒（Axis-Aligned Bounding Box, AABB），长方体的每一轴都是沿着坐标轴的，它计算简单。

如何判断光线和盒子相交？

包围盒一共有6个面，两两相对，构成三组对面，我们将这6个面看作是无限延伸的，那么和包围盒求交的主要思路是：

只有当光线进入每组对面时，光线才进入了包围盒
只要光线离开任意一组对面，光线就离开了包围盒

对于每组对面，都能求出光线进入和离开的时间 \(t_{min}\) 和 \(t_{max}\)，负值也ok（负值代表光线反向传播），光线进入包围盒的时间是三组对面中最大的 \(t_{min}\)，光线离开包围盒的时间是三组对面中最小的 \(t_{max}\)，即，

\[ t_{enter} = \max(t_{min}) \]

\[ t_{exit} = \min(t_{max}) \]

从几何的角度来看，光线和每组对面相交构成一个线段，共形成三个线段，对三个线段求交，得到的线段的起点和终点分别对应 \(t_{enter}\) 和 \(t_{exit}\)。

当 \(t_{enter} < t_{exit}\) 时，说明光线和包围盒相交，反之，不相交。

现在考虑负值的情况

当 \(t_{exit} < 0\) 时，说明包围盒在光线传播方向的背后，光线和包围盒不相交。
当 \(t_{enter} < 0\) 且 \(t_{exit} > 0\) 时，说明光线从包围盒内部发出，光线和包围盒相交。

结论，当 \(t_{enter} < t_{exit}\) 且 \(t_{exit} > 0\) 时，说明光线和包围盒相交，反之，不相交。

AABB包围盒的好处

包围盒是和坐标轴对齐，比如，我们要计算一条光线和垂直于x轴的对面的交点，求交公式可以简化为：

\[ t = \frac{\mathbf{p}'_x - \mathbf{o}_x}{\mathbf{d}_x} \]

只需要用这些点和向量的x分量计算就行了，原因是这组对面的法线 \(N\) 刚好就是x轴方向的单位向量，和 \(N\) 做点积得到的就是x分量。

在对包围盒求交后，如果光线和包围盒相交，那么就要计算光线和包围盒内部的物体求交，如何加速这个过程呢，这就要用到均匀网格（Uniform Grids）和空间划分（Spatial Partitions），这是两种加速计算光线和物体求交的方法。

均匀网格（Uniform Grids）

首先，对包围盒做预处理：

构造包围盒。
建立网格。
标记和物体表面相交的格子。

然后，光线追踪求交

光线穿过包围盒，和每个格子求交（这个计算比直接和物体求交快）。
经过被标记的格子时，光线是有可能和物体产生交点的。
检查光线是否和上一步骤中被标记格子中的物体表面相交。

光线穿过包围盒时，要去判断光线经过哪些格子，这有点类似光栅化时，对直线进行采样的过程，三维空间也有类似二维空间的直线光栅化算法（这个略过）。

为了最优化光线和场景求交的速度，格子不能太多也不能太少，一个经验值是，在3D场景下，格子数目 = 27 * 物体数目。

空间划分（Spatial Partitions）

场景中的物体分布比较稀疏或者比较不均匀时，均匀网格就仍然会产生很多没必要的计算消耗，这时就可以用空间划分的方法。

空间划分的思路是，将包围盒按照树状结构划分，光线和格子求交的时候，按照树的结构计算，即使剪纸，能减少很多计算。

下图列出了三种空间划分方法（简化成二维的形式），分别是八叉树（Oct-Tree），KD树（KD-Tree），BSP树（BSP-Tree）。

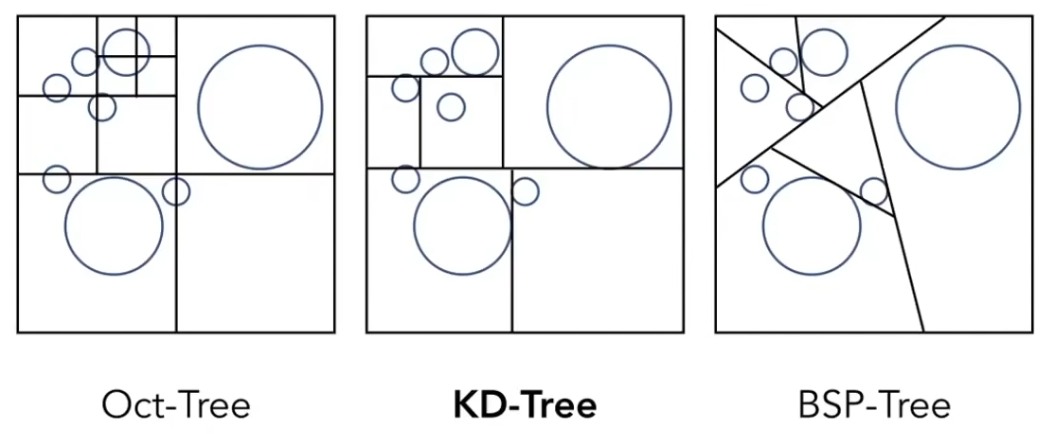
八叉树是将空间递归地划分为8个子空间，直到每个子空间内的物体数目小于某个阈值（在二维空间中，就退化为了四叉树）

KD树是将空间递归地划分为两个子空间，划分的平面是和坐标轴对齐的，他是一个二叉树。

BSP树是将空间递归地划分为两个子空间，划分的平面可以是任意方向的。

KD树是最简单的。

KD树构造了一颗二叉树，光线和包围盒求交时，按照树的结构，依次和每个中间节点和叶节点求交，如果发现中间节点和光线没有交点，就跳过这个子树，和叶节点求交时，如果发现和叶节点的空间有交点，才会去和叶节点内部的物体表面求交。

空间划分的问题：

划分格子时有可能把物体切开，很难判断一个格子和场景中的物体是否相交。
一个物体有可能和多个格子相交。

物体划分（Object Partition）和层次包围盒（Bounding Volume Hierarchy, BVH）

BVH是广泛使用的光线追踪加速结构。

BVH划分的不是空间，是物体，可以理解为对包围盒中的三角形分组，然后对每组三角形重新构造包围盒，划分时，还是以二叉树的结构划分，当叶子节点里面包含的三角形足够少时，就停止划分。

这样，一个物体只可能在一个格子里。

如何划分一个格子呢？

每次划分时都换一个坐标轴。
每次划分最长的一轴。
取位置在中间的三角形，以这个三角形为界划分，保证划分后的两个区域中三角形数量差不多，尽量保证构建出来的树是一个平衡二叉树。快速划分算法可以在O(n)时间复杂度内找到三角形重心的中位数，从而快速找到位置在中间的三角形。

辐射度量学（Basic Radiometry）

不同于Whitted-Style的光线追踪技术。

辐射度量学精确地描述光和物体表面之间的作用，不像Blinn-Phong光照模型中对光强度之类的参数随便给定一个经验值。

它定义了一系列物理光学属性，例如，

Radiant Flux：辐射通量
Intensity：辐射强度
Irradiance：辐射照度
Radiance：辐射亮度

Radiant Energy

能量，单位是\(\mathrm{J}\)焦耳

\[ Q\;[\mathrm{J}=\text{Joule}] \]

Radiant Flux

单位时间的能量，又叫功率（Power），单位是瓦特（W），在光学上叫流明（Lumen）。

\[ \Phi \equiv \frac{\mathrm{d}Q}{\mathrm{d}t}\;[\mathrm{W}=\text{Watt}]\;[\mathrm{lm}=\text{lumen}]^{*} \]

Intensity

度量光源发射出的光能量。

Intensity指某个立体角（Solid angle）的功率（Power）（ω代表立体角）：

\[ I(\omega) \equiv \frac{\mathrm{d}\Phi}{\mathrm{d}\omega} \]

单位是坎德拉（Candela）（sr是立体角的单位）：

\[ \left[\frac{\mathrm{W}}{\mathrm{sr}}\right]\;\left[\frac{\mathrm{lm}}{\mathrm{sr}}=\mathrm{cd}=\text{candela}\right] \]

什么是立体角？

通常的角是用弧度定义的，

\[\theta = \frac{l}{r}\]

三维空间中的角叫立体角，\(A\) 代表球面面积

\[\Omega = \frac{A}{r^2}\]

单位立体角是指单位球面对应的立体角，怎么定义单位球面呢？

用 \(\theta\) 表示和z轴的夹角，用 \(\phi\) 表示绕z轴的旋转角度，用这两个角度，可以定义球面上的一个方向。

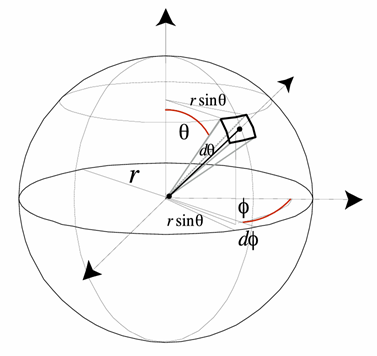
那么单位面积为，

\[ \mathrm{d}A = (r\,\mathrm{d}\theta)(r\sin\theta\,\mathrm{d}\phi) = r^{2}\sin\theta\,\mathrm{d}\theta\,\mathrm{d}\phi \]

单位立体角为,

\[ \mathrm{d}\omega = \frac{\mathrm{d}A}{r^{2}} = \sin\theta\,\mathrm{d}\theta\,\mathrm{d}\phi \]

显然，如果对单位立体角做二重积分（\(\theta\)的范围是\([0,\pi]\)，\(\phi\)的范围是\([0,2\pi]\)），得到的就是球的表面积 \(4\pi\)

所以，Flux 和 Intensity之间的关系为：

\[\phi = 4\pi I\]

（这是个很直观的结论）

Irradiance

度量物体表面接收到的光能量。

Irradiance指单位面积上接收到的功率。

\[ E(x) \equiv \frac{\mathrm{d}\Phi(x)}{\mathrm{d}A} \]

单位是Lux：

\[ \left[\frac{\mathrm{W}}{\mathrm{m}^2}\right]\;\left[\frac{\mathrm{lm}}{\mathrm{m}^2}=\mathrm{lux}\right] \]

这个面积必须垂直于光线方向，如果平面不垂直于光线方向，那么将平面投影到光线的垂直方向上后的面积才是有效面积。

前面介绍Blinn-Phong光照模型时，提到过光的强度衰减，实际上并不准确，在辐射度量学中，衰减的实际上是Irradiance，球面上的一点接收到的功率是：

\[ E' = \frac{\Phi}{4\pi r^2} \]

其中，\(\frac{\Phi}{4\pi}\) 是半径为1的球面上每个点接收到的功率。

下面讲的能量一般都是指 Intensity 和 Irradiance，也就是功率。

Radiance

度量光传播过程中的光能量。

Radiance是指表面发射、反射、透射或接收的功率，单位为单位立体角内的单位投影面积。

\[ L(p,\omega) \equiv \frac{\mathrm{d}^{2}\Phi(p,\omega)}{\mathrm{d}\omega\,\mathrm{d}A\,\cos\theta} \]

其中，\(\theta\) 是光线和表面法线的夹角，或者说，是平面向垂直于光线方向的投影角。

\[ \left[ \frac{\mathrm{W}}{\mathrm{sr}\,\mathrm{m}^{2}} \right]\quad \left[ \frac{\mathrm{cd}}{\mathrm{m}^{2}} = \frac{\mathrm{lm}}{\mathrm{sr}\,\mathrm{m}^{2}} = \mathrm{nit} \right] \]

Radiance可以理解为单位立体角上的Irradiance。

即入射辐射（Incident Radiance），单位面积上接收到的能量在\(\omega\)方向上的部分：

\[ L(p,\omega) = \frac{\mathrm{d}E(p)}{\mathrm{d}\omega\,\cos\theta} \]

\(p\) 是表面上的一个点，\(\omega\) 是入射光的方向。

Radiance也可以理解为单位面积上的Intensity。

即出射辐射（Exiting Radiance），\(\omega\)方向上发出的能量在单位面积上的部分：

\[ L(p,\omega) = \frac{\mathrm{d}I(p,\omega)}{\mathrm{d}A\,\cos\theta} \]

\(p\) 是表面上的一个点，\(\omega\) 是出射光的方向。

Radiance和Irradiance的区别是，Irradiance是单位面积上接收到的总功率，而Radiance是Irradiance在某个方向上的功率。

对Radiance在单位半球面上做积分，就能得到Irradiance。

双向反射分布函数（Bidirectional Reflectance Distribution Function, BRDF）

一束入射光，会向多个不同方向反射，入射光的 Radiance 会在单位表面转换为能量（Irradiance），然后沿某个方向反射出去，转换为该方向上的 Radiance。

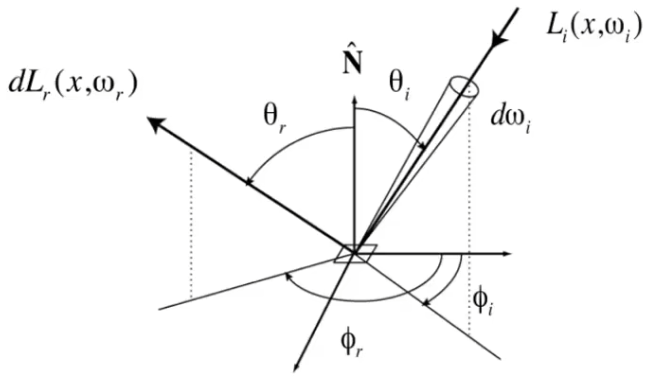
假设打到物体表面上单位面积的 Irradiance为 \(E\)，那么可以将 \(E\) 与入射和出射的 Radiance 联系起来：

从 \(\omega_i\) 方向的入射光满足：

\[ \mathrm{d}E(\omega_i) = L(\omega_i)\cos\theta_i\,\mathrm{d}\omega_i \]

从 \(\omega_r\) 方向的反射光 Radiance 为 \(L_r(\omega_r)\)

BRDF计算了从 \(\omega_i\) 方向入射光的 Irradiance，有多少比例会被反射到 \(\omega_r\) 方向：

\[ f_r(\omega_i \rightarrow \omega_r) = \frac{\mathrm{d}L_r(\omega_r)}{\mathrm{d}E_i(\omega_i)} = \frac{\mathrm{d}L_r(\omega_r)}{L_i(\omega_i)\,\cos\theta_i\,\mathrm{d}\omega_i} \;\left[\frac{1}{\mathrm{sr}}\right] \]

反射方程

从反射光的角度来看，一束反射光是由所有不同角度的入射光在反射方向的分量叠加起来的：

\[ L_r(p,\omega_r) = \int_{H^2} f_r(p,\omega_i \rightarrow \omega_r)\, L_i(p,\omega_i)\, \cos\theta_i\, \mathrm{d}\omega_i \]

一个反射光对应的入射光不一定是光源，也有可能是其他物体表面的反射光，因此，这个计算过程是递归的。

渲染方程

\[ L_o(p,\omega_o)=L_e(p,\omega_o)+\int_{\Omega^{+}} L_i(p,\omega_i)\,f_r(p,\omega_i,\omega_o)\,(\mathbf{n}\cdot\omega_i)\,\mathrm{d}\omega_i \]

\(L_e(p,\omega_o)\) 是物体表面的自发光，公式后半部分是物体表面的反射光。

如果只有一个或多个点光源，其实不需要积分，可以直接求和，如果是个面光源，就需要积分，相当于将面光源视为无数个点光源的集合。

考虑其他物体的反射光作为光源的情况，\(L_r(x',-\omega_i)\) 是其他物体上的一点 \(x'\)，沿着 \(-\omega_i\) 方向反射过来的 Radiance，我们直接将其作为当前点 \(x\) 的入射 Radiance，注意这里为什么要给 \(\omega_i\) 加个负号，是因为在反射方程中，\(\omega_i\) 是指从点 \(x\) 指向光源的方向，加上负号才能正确表示从其他物体的反射点 \(x'\) 指向点 \(x\) 的方向。

\[ L_r(x,\omega_r)=L_e(x,\omega_r)+\int_{\Omega} L_r(x',-\omega_i)\,f(x,\omega_i,\omega_r)\,\cos\theta_i\,\mathrm{d}\omega_i \]

写成简化的形式，用 \(u\) 和 \(v\) 分别表示当前反射点和其他物体的反射点：

\[ L(u)=e(u)+\int L(v)\,K(u,v)\,\mathrm{d}v \]

进一步，可以简写为：

\[ L = E + K L \]

公式后半部分里的 \(L\) 是所有光源直接或间接照射到物体表面的 Radiance。

经过变换，可以得到：

\[ L = (I + K + K^{2} + K^{3} + \cdots)E \]

\[ L = E + KE + K^{2}E + K^{3}E + \cdots \]

其中，\(K^{n}E\) 是光源发出的光经过多次反射后到达物体表面的 Radiance。

全局光照

光线弹射一次叫直接光照，光线弹射多次叫间接光照，这些光照的总和叫全局光照，也就是上面最后定义的 \(L\)。

光栅化只能处理直接光照，即物体的自发光+光源一次照射。

概率论回顾

\(X\)，随机变量（Random Variable），取值不确定的变量, 比如骰子可以取1~6六个值。

\(X \sim p(x)\)，概率密度函数（Probability Density Function, PDF），描述随机过程取某个值 \(x\) 的概率。

期望值（Expected Value），随机变量理论上的平均值，对概率的加权平均。

\[ E[X] = \sum_{i=1}^{n} x_i\,p_i \]

对概率密度函数 \(p(x)\) 做积分的结果是1，

\[ \int p(x)\,\mathrm{d}x = 1 \]

用 \(p(x)\) 求数学期望，

\[ E[X] = \int xp(x)\,\mathrm{d}x \]

蒙特卡洛积分（Monte Carlo Integration）

蒙特卡洛积分是一种积分方法，如果我们想求一个复杂函数 \(f(x)\) 在区间 \([a,b]\) 上的积分：

\[ \int_{a}^{b} f(x)\,\mathrm{d}x \]

在区间 \([a,b]\) 上根据某个概率密度函数 \(p(x)\) 对 \(x\) 采样 \(N\) 个点，

\[ F_N = \frac{1}{N}\sum_{i=1}^{N}\frac{f(X_i)}{p(X_i)} \]

\(F_N\) 就是对积分的估计。

如果 \(p(x)\) 是均匀分布，且在区间 \([a,b]\) 上的概率总和为1，那么\(p(x) = \frac{1}{b-a}\)，\(F_N\) 为：

\[F_N = \frac{b-a}{N}\sum_{i=1}^{N} f(X_i)\]

可以这么理解上面这个解法，在区间 \([a,b]\) 上采样一个点 \(x_i\)，计算 \(f(x_i)\)，然后将 \(f(x_i)\) 乘以区间长度 \((b-a)\)，得到这个点对应的面积，然后对所有采样点的面积求平均。

路径追踪（Path Tracing）

利用蒙特卡洛积分求解渲染方程

光滑的反射有两种，

镜面反射（Specular/Mirror Reflection）：光线按照入射角等于反射角的方式反射。
光泽反射（Glossy Reflection）：有反射，有高光，但表面不是完全光滑（比如带点磨砂质感）。

whitted-style光线追踪有一些固有的问题，例如：

只能处理镜面反射，不能处理光泽反射。
光线反射到漫反射材质时就停止了。

辐射度量学渲染方程可以解决这些问题。

使用蒙特卡洛积分来求解渲染方程

假设有一个面光源在照射物体，在半球面 \(\Omega^{+}\) 上，对 \(\omega_i\) 均匀采样，对应的概率密度函数为 \(p(\omega_i) = 1/2\pi\)。（半球的面积是 \(2\pi\)）

\[ L_o(point,\omega_o)=\int_{\Omega^{+}} L_i(point,\omega_i)\,f_r(point,\omega_i,\omega_o)\,(\mathbf{n}\cdot\omega_i)\,\mathrm{d}\omega_i \\ \approx \frac{1}{N}\sum_{i=1}^{N}\frac{L_i(point,\omega_i)\,f_r(point,\omega_i,\omega_o)\,(\mathbf{n}\cdot\omega_i)}{p(\omega_i)} \]

可以用入射光的数量作为采样点的数量 \(N\)。

其他物体反射到当前物体表面的光照怎么计算呢？递归地计算其他物体表面的反射光，然后将其作为当前物体的入射光就好了。

路径追踪

问题是，每次光线反射，都会新增 N 个光线，计算量会爆炸式增长，怎么办？

最简单的办法是，每次反射时只随机采样一个光线，即 \(N=1\)，这样，每次光线反射时，只会新增一个光线，计算量不会爆炸式增长。

\(N=1\) 时反射过程就叫做路径追踪（Path Tracing），\(N \neq 1\) 时叫做分布式路径追踪（Distributed Path Tracing）。

采样点太少的问题可以通过增加入射光线的数量来解决（增加采样次数），这很好理解，反射光线变少了，那就增加入射光线的数量。

俄罗斯轮盘赌（Russian Roulette）

递归过程什么时候停止呢？如果简单指定一个最大递归深度，可能会导致一些光线路径被截断（相当于产生了能量损失），影响渲染质量。

一种更好的办法是俄罗斯轮盘赌（Russian Roulette）方法，在每次反射时，给光线一个存活概率 \(P\)，以概率 \(P\) 继续反射，以概率 \(1-P\) 停止反射，反射时，对光出射能量做一个放大，以补偿停止反射带来的能量损失，使 \(L_o\) 满足：

\[L_o = P(L_o / P) + (1-P)*0\]

对光源采样

路径追踪中，每个反射点只有一条反射光线，并且反射方向是随机的，因此，光源越小，光线直接打到光源的概率就越小，导致噪点增多，如果向四周均匀采样，则会造成很多计算上的浪费。

解决办法，生成反射光线时，不再采用均匀分布，而是直接在光源上采样。

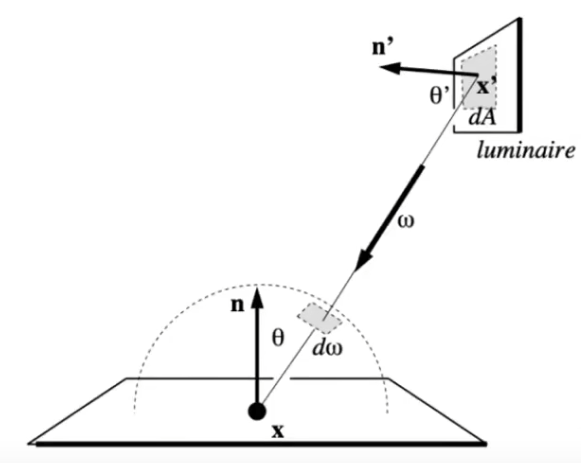
为此，我们需要将渲染方程改写为在光源上做积分的形式，对积分进行换元，将 \(d\omega\) 换成 \(dA\)。

根据上图及立体角的定义，可以得到以下关系：

\[ \mathrm{d}\omega = \frac{\mathrm{d}A \cos\theta'}{\lVert x' - x \rVert^{2}} \]

积分换元：

\[ L_o(x,\omega_o) = \int_{\Omega^{+}} L_i(x,\omega_i)\,f_r(x,\omega_i,\omega_o)\,\cos\theta\,\mathrm{d}\omega_i \\ = \int_{A} L_i(x,\omega_i)\,f_r(x,\omega_i,\omega_o)\,\frac{\cos\theta\,\cos\theta'}{\lVert x' - x \rVert^{2}}\,\mathrm{d}A \]

在计算着色点的反射时，将光照分为两部分，光源的直接贡献和其他物体的间接贡献，在光源上均匀采样，对于其他物体，仍然是使用俄罗斯轮盘赌的方法递归计算。

关于辐射度量学的个人理解

Intensity、Irradiance、Radiance这三者的关系可以这么理解，Intensity 和 Irradiance 转换为 Radiance 时，都需要引入 \(\cos\theta\)，\(\cos\theta\) 是接收光线的表面法线和入射光线的夹角，引入 \(\cos\theta\) 的原因是，接收光线的平面可能不垂直于入射光线，这会使入射光线能量产生一定的衰减，\(\cos\theta\) 就反映了这个衰减。

关于光源采样算法的个人理解

对光源采样的时候，做了一个积分换元，这里要注意，换元同时也使积分上下限（积分范围）产生了变化，在没有对直接光照和间接光照做拆分时，积分变量是 \(\omega_i\)，积分范围是半球面，积分做拆分后，对直接光照的积分改为了对光源表面 \(dA\) 做积分，积分范围是整个光源表面，这相当于是把原积分变量 \(\omega_i\) 的范围限制到了光源表面和光线接收点的夹角范围，不再是个半球面，当然这不是什么问题，这正是我们所期望的。

关于对点光源和面光源的个人理解

换元时，又引入了一个 \(\cos\theta'\)，这是入射光线和光源表面法向量的夹角，这又体现了一次光线能量的衰减，这个衰减源于光源是一个平面，上面我们讨论辐射度量学时，是把光源作为点光源来看待的，不存在这个问题。

课程中提到，从算法实现的角度上来讲，如果场景中是个点光源，我们得把它看作是一个极小的面光源来看待，这实际上是对算法设计的简化，我认为虽然我们把点光源当作一个面光源来处理，但要保持点光源向四面八方发光的特性，即，\(\cos\theta'\) 应恒为1，点光源平面的法向量应该永远和光线方向相同，不应该有能量的衰减。

点光源和面光源体现的是图形学算法在数学上对真实物理世界光源做出了不同的抽象，我们应该注意到，上面的图形学算法是把面光源抽象为一个光线具有方向的平面，并且只有正面能发光，向两侧发光时，光线能量会有衰减，基于这个前提，上面的积分公式才能成立。

因此，根据我的理解，如果场景中是一个点光源，我们应该认为它的法线方向和光线方向永远一致，这才符合点光源的发光特性。

（以上理解没有经过实验验证，仅仅是设想。）