《线性代数(第6版)》学习笔记
《线性代数(第6版)》由Gilbert Strang(吉尔伯特·斯特朗)编写,是线性代数领域的经典教材。
这个笔记的内容来自MIT的线性代数课程以及《线性代数(第6版)》这本教材。
线性方程组的几何解释
线性组合
我们可以将其表示为矩阵形式:
我们可以将其记为 \(Ax=b\)。
站在行的角度来看,这个方程组中的每个方程都可以确定一条直线,方程组是在求两条直线的交点。
站在列的角度来看,它的列视图可以表示为:
这实际上是两个列向量的线性组合(Linear Combination)。
考虑以下三元线性方程组
和二元线性方程组同理,站在行的角度,每个方程都可以确定一个平面,方程组是在求三个平面的交点。站在列的角度,可以将方程组表示为 \(Ax = b\)。
奇异/不可逆
站在列的角度,考虑这样一个问题,对于 \(Ax = b\),是不是对于任意的 \(b\),都存在解 \(x\) 呢?换句话说,列向量的线性组合能否覆盖整个三维空间?
假设三个列向量处于同一个平面内,答案就是否定的,一个平面外的向量必然不能被这三个列向量的线性组合表示出来。这种情况,我们称之为奇异(Singular)或矩阵不可逆(Invertible)。(原因在于这三个列向量不是完全相互独立的)
矩阵乘向量
两种方法:
- 将矩阵的每一行与向量做点积
- 将矩阵的列向量与向量的每个分量做线性组合
矩阵消元(Elimination)
消元和回代
矩阵消元是让每个方程组消去一个未知数,使系数矩阵成为一个上三角矩阵 \(U\)(又叫高斯消元法)。
考虑以下线性方程组:
我们可以将其表示为矩阵相乘形式 \(Ax = b\)
消元法要将系数矩阵 \(A\) 变为上三角矩阵 \(U\):
对角线上的元素称为主元(Pivot),主元不能是0。
如果主元的数量不够,少于未知数的数量,意味着消元法失效了。
回代(Back Substitution)
将线性方程组等号右侧的 \(b\) 加入到系数矩阵中,新的矩阵称为增广矩阵(Augmented Matrix),对增广矩阵做消元法,最右侧一列会同步变化,我们将新的一列记为 \(c\):
有了三角形式的增广矩阵,我们就可以从最后一个方程开始,由下往上依次将未知数带入到方程组中,求解出未知数,最后这个代入并求解的过程,叫做回代。
矩阵乘法的列视角和行视角
根据上述内容,矩阵 A 乘以一个列向量 b ,实际上是A 的列向量的线性组合,以 b 的各分量为系数,最终得到一个列向量。
站在行视角来看,一个行向量 r 乘以矩阵 A ,实际上是 A 的行向量的线性组合,以 r 的各分量为系数,最终得到一个行向量。
为什么这里要提出矩阵乘法的行视角呢?因为上述消元法实际上是对矩阵的行做线性组合,因此,利用矩阵乘法的行视角,我们可以将消元法表示为一个矩阵乘法的形式。
上一节中的一系列消元步骤,可以表示为:
左侧的两个矩阵称为初等矩阵(Elementary Matrix)或消元矩阵(Elimination Matrix),记作 \(E\),它表示对矩阵做了一次行操作/行变换,\(E_{ij}\) 表示要消去原矩阵第 i 行、第 j 列的元素。
(假设有一个矩阵乘法 AB = C,现在已知 B 和 C,要求出 A,站在列的视角,可以将 A 视为一组新的基向量,站在行的视角,可以将 A 是为对 B 做一系列行变换的矩阵,这两种方法都能快速得到A)。
置换矩阵(Permutation Matrix)是一种特殊的初等矩阵,用于交换矩阵的行或列,交换单位矩阵的对应行即可得到置换矩阵。
两个矩阵相乘,左侧矩阵是对右侧矩阵做行变换,右侧矩阵是对左侧矩阵做列变换。
(注意,这里提到的行变换和列变换是针对整个矩阵而言的,而线性变换是针对向量而言的。)
矩阵乘法满足结合律,但不满足交换律。
矩阵乘法和逆
矩阵乘法
矩阵乘法 AB = C 的五种计算方法:
- 对 A 的单行和 B 的单列做点积
- 将 AB = C 视为 A 的列向量的线性组合,B 的每一列是 C 的对应列的系数
- 将 AB = C 视为 B 的行向量的线性组合,A 的每一行是 C 的对应行的系数
- 对 A 的单列和 B 的单行做矩阵乘法,然后对所有结果求和,假设 A 有 n 列,B 有 n 行,那么结果是对 n 个矩阵求和。
- 分块乘法。
以下是方法 4 的一个例子:
先来看单列和单行相乘的结果:
实际上是对左边的列向量或右边的行向量做了按倍数放大操作,这些向量的方向都是同一方向,而且没有发生变化,这个矩阵的行空间和列空间都在同一条直线上。
矩阵的逆(Inverse)
\(A^{-1}A = I\)
如果 A 是方阵,则 \(AA^{-1} = I\)
A 叫做可逆矩阵或非奇异矩阵。
逆矩阵不一定存在。
判断一个矩阵是否可逆(例如 \(A = \begin{bmatrix} 1 & 2 \\ 3 & 6 \\ \end{bmatrix}\) )有以下方法:
- 行列式为0,则矩阵不可逆
- 考虑是否存在一个矩阵和它相乘能够得到一个单位矩阵,由于它是个方阵,既可以考虑把它放在左边的情况,也可以考虑放在右边的情况。
- 考虑是否存在一个非零向量x,使得 Ax = 0 ,如果存在这样的非零向量x,则矩阵A不可逆。一方面从线性方程组的角度来看,如果 A 可逆,它的主元数量应该等于未知数的数量,Ax = 0 只有零解,x 不会是非零向量,另一方面,从线性组合的角度来看,一个可逆的矩阵,它的列向量是线性无关的,不可能通过线性组合得到零向量,除非所有系数都是零。如果 A 存在逆矩阵,可以在方程 Ax = 0 左右两侧同时乘以 A的逆,只能得到 x = 0。
一个不可逆的、奇异的矩阵,它的列向量是线性相关的,可以通过线性组合得到零向量,这意味着 Ax = 0 存在非零解 x。
如果要求一个矩阵的逆,可以利用 \(AA^{-1} = I\) 将问题转化为 求 \(AX = I\) 的问题,其中 X 是未知矩阵,可以将 I 看作是多个列向量组成的矩阵,然后对每个列向量分别求解线性方程组 \(Ax = e_i\),其中 \(e_i\) 是 I 的一个列向量,最终将所有的解组合成矩阵 X 即可。
高斯-约旦消元法(Gauss-Jordan Elimination)也可以用来求矩阵的逆,具体做法是将矩阵 A 和单位矩阵 I 拼接成增广矩阵 [A | I],然后对增广矩阵做行变换,直到左侧的 A 变成单位矩阵,此时右侧的矩阵就是 A 的逆矩阵 \(A^{-1}\)(其实就是上面求解多个线性方程组方法的简化版)。
高斯-约旦消元法可以很容易地从求解线性方程组的角度来理解,还有一种理解方式,假设 \([A | I] \to [I | A']\) 这个变换是由 \(E\) 实现的,即 \(E[A | I] = [I | A']\),那么根据矩阵分块乘法,\(EA = I\),\(EI = A'\),很容易就能得到 \(A' = A^{-1}\)。
两个矩阵相乘的逆,\((AB)^{-1} = B^{-1}A^{-1}\),这很容易证明,\((AB)(AB)^{-1} = I, (AB)(B^{-1}A^{-1}) = A(BB^{-1})A^{-1} = AIA^{-1} = AA^{-1} = I\),这个性质也很容易理解,从线性变换的角度来看,先做 B 变换,再做 A 变换,那么要想倒回去,必须先做 A 的逆变换,再做 B 的逆变换。
矩阵的逆与转置(Transpose) 满足 \((A^T)^{-1} = (A^{-1})^T\), 证明也很简单,\(AA^{-1} = I = I^T = (AA^{-1})^T = (A^{-1})^TA^T\),由 \((A^{-1})^TA^T = I\) 可以得到 \(A^T\) 和 \((A^{-1})^T\) 互为逆。这里用到一个转置性质:\((AB)^T = B^TA^T\)。
矩阵分解(A = LU)
怎么分解
假如 2x2 矩阵 A 通过一次行变换 \(E_{21}\) 消元,变成了上三角矩阵 U,即 \(E_{21}A = U\),现在我们想知道如何从 U 反向变回 A,也就是存在一个 L 使得 A = LU,L 是 \(E_{21}\) 的逆矩阵。(U 是个上三角矩阵,L 是个下三角矩阵)
例如:
上面这个例子不仅将 A 分解成了 LU 的形式,还进一步分解成了 LDU 的形式,其中 D 是一个对角矩阵。
如果 A 是 3x3 矩阵,会复杂一些,\(E_{32}E_{31}E_{21}A = U, A = L U,L = E_{21}^{-1}E_{31}^{-1}E_{32}^{-1}\)。
假设有一个 3x3 矩阵 A,它的第三行第一列元素为0,那么它在消元时只需要做两次行变换 \(E_{32}E_{21}A = U\),对应的 L 矩阵为 \(L = E_{21}^{-1}E_{32}^{-1}\),如下所示:
我们发现一个问题,虽然我们没有做 \(E_{31}\) 这个行变换,但是 E 矩阵的第三行第一列元素并不是0,而 L 矩阵的好处在于,它的元素中只会把消元时用到的乘数(消元过程中需要乘以并减去的那个倍数)记录下来,其他位置的元素都是0或1(前提是没有行交换这种变换),换句话说,只要我知道所有的消元乘数,就能快速得到 L,并且,L的对角线上的元素都是 1。
消元的计算复杂度
一个 nxn 矩阵消元,如果对一个元素做一次乘法和减法算一次操作,总共进行了多少次消元操作?
假设矩阵中的所有的非主元都不为0,都需要消元,如果要把第一列所有的非主元都消掉,那么矩阵中除了第一行之外的所有行都需要做一次消元操作,因此总共有 n(n-1) 个元素会发生变化,以此类推,把第二列的所有非主元都消掉,共有 (n-1)(n-2) 个元素会发生变化,我们把计算简化一下,把 n(n-1) 视为 \(n^2\),把(n-1)(n-2) 视为 \((n-1)^2\),总的操作次数大约有 \(n^2 + (n-1)^2 + ... + 1\) 这么多次,整体为 \(n^3\) 这个量级,实际大约是 \(\frac{1}{3}n^3\)(直接对 \(x^2\) 求积分可以得出,级数可以理解为用宽度为1的矩形和去对积分做近似)。
行交换、置换和转置
置换和转置
现在我们把行交换也考虑进去,当某一行的主元为 0 时,就需要行交换,行交换需要使用置换矩阵。
前面讲过,置换矩阵实际上是把单位矩阵的行交换得到的矩阵,3x3 矩阵的置换矩阵有 6 种,如果这 6 个置换矩阵互相相乘,得到的新矩阵仍然是这6 个置换矩阵中的一个,也就是说这 6 个置换矩阵在矩阵乘法下构成了一个群。
(注意,这 6 个置换矩阵可不都是仅交换两行的,有可能一个置换矩阵交换了多行,它们都是对行的重排列)
一个 nxn 的矩阵有 n! 种置换矩阵,即 \(A_{n}^{n}\) 种行排列方式。
用 P 表示置换矩阵,上节中的矩阵分解可以表示为一般形式 PA = LU,用来包括消元时需要做行交换的情况。
置换矩阵的逆就是它的转置,\(P^{-1} = P^T\),这也意味着 \(P^TP = I\)
对称和转置
对称矩阵(Symmetric Matrix)满足 \(A = A^T\),对称矩阵的逆矩阵也是对称矩阵,很容易证明,\(A^{-1} = (A^T)^{-1} = (A^{-1})^T\)。
任意一个矩阵和它的转置相乘(\(A^TA\))就可以得到一个对称矩阵,可以这样证明,\((A^TA)^T = A^T(A^T)^T = A^TA\)。
向量空间
向量空间
标量和向量,标量就是一个数,向量是一个有方向和大小的量,可以用有序数组表示。
\(R^2\) 就是一个向量空间,它表示所有二维实向量的集合。
向量空间必须对数乘和加法这两种运算封闭(对线性组合封闭)
子空间(Subspace)
子空间也必须满足对数乘和加法这两种运算封闭。
例如,在 \(R^2\) 中,一条过原点的直线就是一个子空间,因为这条直线上的所有向量都对数乘和加法封闭,如果这条直线不过原点,那它就不是子空间。
实际上,\(R^2\) 有三种子空间,(1)它本身,(2)过原点的直线,(3)零点。
\(R^3\) 有四种子空间,(1)它本身,(2)过原点的平面,(3)过原点的直线,(4)零点。
如果从一个 n 行矩阵 A 的列向量出发构造子空间,A 的列向量的所有线性组合会构成一个 \(R^n\) 的子空间,这个子空间称为列空间,用 \(C(A)\) 表示。
在 \(R^3\) 中,两个线性无关的列向量构成的列空间是一个过原点的平面。
如果是两个共线的向量,它们构成的列空间就是一条过原点的直线。
两个子空间的并集不一定是一个新的子空间。
两个子空间的交集仍然是一个子空间,因为交集中的向量必然同时属于两个子空间,它们数乘和相加后的结果也必然属于两个子空间,也就是说,数乘和相加后的结果仍在交集之中。
列空间(Column Space)
一个 mxn 矩阵,例如一个 4x3 矩阵 A,A 的列向量本身位于 \(R^4\) 中,它的列空间 \(C(A)\) 是 \(R^4\) 的一个子空间。
我们把它和线性方程组 Ax = b 联系起来看,b 必须位于 A 的列空间 \(C(A)\) 中,方程组才有解。
例子中,对于任意的b,Ax = b 并不是都有解,它有四个方程,但只有三个未知数,三个列向量的线性组合最多只能张成一个三维空间,无法覆盖整个四维空间,因此,只有当 b 是 A 的列向量的线性组合时,Ax = b 才有解。
如果 A 的三个列向量是线性相关的,只有两个线性无关的列向量,那么能表示的 b 就更少了,我们把两个线性无关向量称为主列,它们张成的子空间是 \(R^4\) 的一个二维子空间。
零空间(Null Space)
当 b 为 0 向量时,方程组变成 Ax = 0 ,零空间是由 Ax = 0 所有的解 x 组成的子空间,记作 \(N(A)\)。
(要构成子空间,一个解做完数乘和加法后仍然是方程的解,稍微琢磨一下就知道,Ax = 0 的全体解必然是构成一个子空间的。)
以上面的 4x3 矩阵 A 为例,方程中中有四个方程,而未知数只有三个,因此 A 的列空间 \(C(A)\) 是 \(R^4\) 的一个子空间,零空间 \(N(A)\) 是 \(R^3\) 的一个子空间。
零向量必然在零空间中。
把 Ax = 0 换成 Ax = b,它的解不构成一个子空间(最基本地,解中连零向量都不包含)。
向量空间需要穿过零点,不过零点不是向量空间。
注意,列空间是由列向量出发张成的,而零空间是由全体解向量组成的,我们最开始并不知道里面有哪些向量,只能通过解方程组来找到这些向量,这是两种不同的子空间构造方式。
Ax = 0
特解
考虑这样一个 Ax = 0
消元之后会得到
可以看到只有两个主元,我们把两个主元称为矩阵的秩(Rank)为 2。
从 Ax=0 到 Ux=0,解空间(零空间)不会变。
(前面提到,矩阵中线性无关的列叫主列,我们可以观察到,消元结束后,主元所在的列就是主列。)
我们把主元所在的列称作主列(Pivot Column),没有主元的列称作自由列(Free Column)。
自由列对应的未知数的值可以随便取值,然后我们肯定能给主元对应的未知数找到两个值,从而求出方程的解,一组特定的自由变量称为特解。
此时,只要找到两个线性无关的特解,就能将解写成两个特解的线性组合的形式,张成零空间。
如何取特解
简化行阶梯形矩阵(Reduced Row Echelon Form, RREF)是矩阵消元的最简形式,指每个主元都是1,并且主元所在列的其他元素都是0的矩阵。
对于上面的例子,简化行阶梯形矩阵为:
把 R 矩阵列的顺序调整一下,使得 R 变成以下形式:
左侧是由主列构成的单位矩阵,右侧是由自由列构成的矩阵 F。
现在求解 Rx = 0 变成了求解 RN = 0,N 代表零空间矩阵(即 N 的列可以张成整个零空间)。
很容易得到
(我们能够注意到,Ax = 0求特解实际上就是求一组零空间的基,有几个自由变量,就有几个基向量)
Ax = b
求解 Ax = b
Ax = b 可能无解,可能有唯一解,可能有无穷多解。
还是以上面的例子为例,加上 b 之后,可以得到一个增广矩阵
消元后,
并且由于第三行都为0,所以有 \(0 = b_{3}-b_{2}-b_{1}\)。
b 的可解性条件(Solvability Condition)的两种等价描述:
站在列的角度:b 必须属于 A 的列空间。
站在行的角度:如果消元后有一行是全0(例如上面的情况),b 变换后对应的分量必须为0,这个分量实际上是 b 原分量的线性组合。
求解 Ax = b
继续上面的例子,先找特解,将所有自由变量设为0,求出一个特解 \(x_{p}\),然后再在零空间内找一个任意的解 \(x_{n}\),最终的解可以表示为 \(x = x_{p} + x_{n}\)。
通解为 \(x = x_{p} + c_1n_1 + ... + c_nn_n\),即特解加上零空间的线性组合。
上面的例子得到的通解为:
这个通解所代表的一系列向量,并不能构成一个子空间,因为它们并不包含零向量,如果不包含最左边那个特解,剩下的部分是 Ax = b 的零空间(即 Ax = 0 的解空间),它是一个过原点的平面,加上特解以后,相当于整个平面朝着特解的方向整体平移了一段距离。
mxn 矩阵
考虑秩为 r 的 mxn 矩阵 A,主元个数不可能超过行数 m 和列数 n,即,
列满秩
考虑列满秩的情况(r=n,m>n),列全部线性无关,没有自由变量,零空间只有零向量(Ax = 0只有零解),Ax = b 有解时只有唯一解,或者无解(方程只有 0 个解或 1 个解)。
此时,
行满秩
考虑行满秩的情况(r=m,n>m),Ax = b 有无穷多解,对任意的 b,Ax = b 都有解。
此时,
行列都满秩
r = m = n,A 是一个方阵,并且是可逆矩阵,Ax = b 对任意的 b 都有唯一解。
此时,
行列都不满秩
r < m,r < n,Ax = b 有无穷多解或无解,不可能有唯一解。
此时,
线性相关
线性相关(Linear Dependence)、线性无关(Linear Independence)、基(Basis)、维度(Dimension)
Ax = 0 存在非零解的原因是,A 消元后存在自由变量,A 的列向量是线性相关的。
假设 A 中存在一个全 0 的列,那么 A 的列向量的线性组合中全 0 列的系数可以是任意的,Ax = 0 会存在无穷多个解。
当矩阵的零空间中只有零向量时,A 的列向量是线性无关的。
如果 mxn 矩阵的列是线性无关的,矩阵的秩 r = n,秩代表线性无关的列向量的个数。
生成/张成(Span):两个线性无关的向量的线性组合可以张成一个平面。
基向量:一组线性无关的向量,并且张成一个空间,基向量的个数称为空间的维度,只有零向量的空间是 0 维的。
对于矩阵 A,列空间的维数是线性无关的列向量的个数,即矩阵的秩 r(列空间的维数和行数无关)。
零空间的维数是自由变量的个数,即 n - r,Ax = 0 有几个自由向量,就有几个特解。
四个基本子空间
列空间 \(C(A)\)、零空间 \(N(A)\)、行空间(A转置的列空间) \(C(A^T)\)、左零空间(A转置的零空间) \(N(A^T)\)。
假设 A 为 mxn 矩阵,秩为 r,那么这四个子空间的关系如下表所示:
| 子空间 | 子空间所在空间 | 子空间维度 |
|---|---|---|
| 列空间 \(C(A)\) | \(R^m\) | \(r\) |
| 零空间 \(N(A)\) | \(R^n\) | \(n-r\) |
| 行空间 \(C(A^T)\) | \(R^n\) | \(r\) |
| 左零空间 \(N(A^T)\) | \(R^m\) | \(m-r\) |
(注意,子空间所在空间是根据向量的元素个数来定的,而子空间的维度是根据空间中线性无关的基向量个数来定的。)
行空间
矩阵 A 经过消元后变成 R,零空间不变(这是前面讲过的),但是它的列空间变了,\(C(R) \neq C(A)\),而它的行空间没变(因为消元做的是行变化,通过线性组合改变行的值),R 中的前 r 行可以作为行空间的一组基。
左零空间
左零空间 \(N(A^T)\) 是 A 转置的零空间,即 \(A^Ty = 0\) 的解空间。
如果将方程转置,\(A^Ty = 0\),就会变成 \(y^TA = 0\)(这正好符合前面提到的,站在行的角度,左侧向量是右侧矩阵行向量的线性组合系数),这就是为什么 A 转置的零空间叫左零空间,因为 \(y^T\) 在 A 的左侧。
如何求左零空间的基呢?
先求从 A 到 R 的消元矩阵(行变换矩阵) E,利用高斯-约旦消元法,\([A_{m*n}|I_{m*m}]->[R_{m*n}|E_{m*m}]\),我们发现,E 就是 A 的消元矩阵。
然后就能得到 EA = R,R 是行阶梯矩阵,里面可能会存在全 0 行,那么 E 中对应的那一行就是左零空间的一个基,
所有 3x3 矩阵组成的空间
这是一种特殊的向量空间,我们把一个 3x3 矩阵看作一个向量,全体 3x3 矩阵构成一个向量空间,用 M 表示。
其中有几种子空间:所有的上三角矩阵,所有的对称矩阵,所有的对角矩阵(即前两个子空间的交集,前面讲过两个子空间的交集仍然是一个子空间)。
所有对角矩阵组成的子空间维度是3,以下是它的一组基,
以上是一种把 \(R^n\) 扩展到 \(R^{n*n}\) 的一种思想。
对于 \(R^{n*n}\) 空间,有一组标准基(Standard Basis),每个基矩阵中只有一个元素为1,其他元素都为0,总共有 \(n^2\) 个基矩阵, 例如 \(R^{3*3}\) 空间的标准基为:
共有 9 个基矩阵,因而 \(R^{3*3}\) 是一个 9 维空间。
我们用 S 表示所有对称矩阵组成的子空间,用 U 表示所有上三角矩阵组成的子空间,那么 S + U 是整个 \(R^{3*3}\) 空间,即 S + U = M(注意这里不是取 S 和 U 的并集,而是将任一对称矩阵和任一上三角矩阵相加),这里面有一个结论, dim(S) + dim(U) = dim(S ∩ U) + dim(S + U),即 6 + 6 = 3 + 9 ,dim代表空间维度。
微分方程空间
这是一个二阶常系数微分方程:
解方程的目的是求出 y 的函数表达式。
这个方程有两个特解,\(y_1 = \cos x\),\(y_2 = \sin x\),任意的 y 都可以表示为 \(y = c_1 \cos x + c_2 \sin x\),这也是方程的通解。
该微分方程的零空间是一个二维空间,上面两个特解可以构成一组基。
秩为 1 的矩阵
现在已经知道,mxn 矩阵 A 的秩为 r 时,A 的行空间和列空间的维度均为 r。
所有秩为 1 的矩阵都能一列乘以一行的形式,例如:
秩为 1 的矩阵可以看作是一个基本矩阵,例如,一个秩为 4 的矩阵可以由四个秩为 1 的矩阵组合得到。
然而所有秩为 4 的矩阵并不构成一个子空间(按前面所讲,把矩阵视为“向量”,矩阵的集合也能组成一个子空间),如果矩阵不满秩,那么它们的和的秩可能会大于4,实际上,两个矩阵之和的秩不大于两个矩阵的秩之和,\(Rank(A + B) \leqslant Rank(A) + Rank(B)\)。
一个例子
现在有一个向量集合,由所有元素之和为 0 的 4 维向量组成,这显然是一个子空间,从直觉上,我们能给出一组基:
显然,这是个三维子空间。
用 v 表示这个子空间中的一个向量,用 S 表示这个子空间,如果我们将 S 视为矩阵 A 的零空间,那么只要找到一个满足 Av = 0 的 A,就能知道 S 的维度和基向量。
显然,A 只要为一个全 1 的行向量即可,即,\(A = \begin{bmatrix} 1 & 1 & 1 & 1 \end{bmatrix}\),A 的秩为 1,A 的零空间的维度为 4 - 1 = 3,这和我们前面得到的结果是一致的,另外,A 的行空间维度为 1,A 的左零空间维度为 0。
一个图论的例子
假设一个图有 4 个节点,5 条边,我们可以将其表示为一个 5x4 的矩阵 A,行表示边,列表示结点,边有方向,这种矩阵叫关联矩阵(Incidence Matrix),关联矩阵中的元素表示结点和边的连接情况,-1 表示边从该结点出发,1 表示边指向该结点,0 表示该结点和该边不连接。
例如,有以下图:
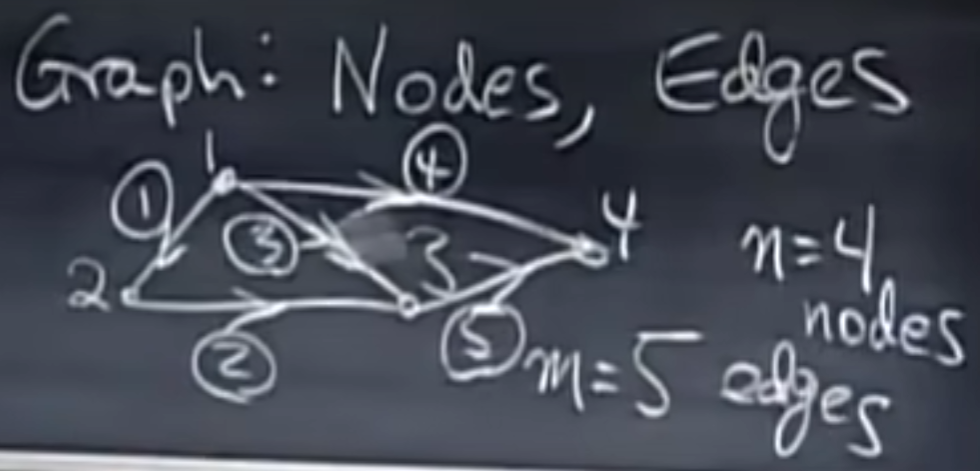
它的关联矩阵为:
前三行对应边 1、2、3,从图中可以看出,边 1、2、3 构成了一个回路(Loop),而在矩阵 A 中,前三行是线性相关的,其实回路就是线性相关的,没有回路时,矩阵的行是线性无关的,这时的图叫做树。
考虑 A 的列空间和零空间,
如果用 \(x_1, x_2, x_3,x_4\) 表示各节点的电势,那么 Ax 表示各边从起点到终点的电势差,Ax = 0 是想求出各节点的电势为多少时,各边的电势差都为0。
我们会发现,除了全零以外,全 1 向量也是 Ax = 0 的解,这意味着所有节点电势相等时,各边的电势差都为0,所以,A 的零空间是 1 维的,这也意味着,只要确定了一个节点的电势,其他三个节点的电势就都确定了,A 的 秩为 3。
考虑 A 的行空间和左零空间,
如果用 \(y_1, y_2, y_3, y_4, y_5\) 表示各边的电流,那么 \(A^Ty\) 表示各节点的电流总和,\(A^Ty = 0\) 是想求出各边的电流为多少时,各节点的电流总和都为0。
\(A^Ty = 0\) 就是基尔霍夫电流定律(KCL),即每个节点上的合电流为0。
左零空间的维度为2,即 m-r=5-3=2,这意味着可以找到两组线性无关的解,这也意味着,可以在图中找到两条独立的回路。
抛开物理意义,从几何上来看,任何一个图的拓扑结构都满足这个规律,即独立回路的数量 = \(dim(N(A^T))\) = m - r = 边数 - (节点数 - 1) = 边数 - 节点数 + 1,这个规律也叫欧拉公式(Euler's Formula),这里是以线性代数的视角来看待这个问题。
回到上面的电路例子,根据欧姆定律,我们有 电流 = 常数*电势差,这个常数是电导(电阻的倒数),即 \(y = Ce\),如果考虑外部的电源,输入电流 f 或输入电压 e,系统的总电势差和电流和则不再为0,会有\(Ax = e\),\(A^Ty = f\),最终能够得到一个平衡方程:\(A^TCAx = f\),\(A^TCA\) 总是对称的。
复习1
如果 \(B^2 = 0\),那么 \(B 不一定为 0\),例如:
如果 C 是一个可逆矩阵,CBx=0 和 Bx=0 有相同的解,换句话说,CB 和 B 有相同的零空间。
如果一个矩阵交换了两行,那么它的行空间没有变,零空间没有变,列空间变了,左零空间变了。
一个向量不可能既在零空间中,又在行空间中,零空间和行空间的交集中只有零向量。
正交(Orthogonality)
矩阵 A 的四个子空间中,行空间和零空间正交,列空间和左零空间正交。
正交向量
正交向量(Orthogonal Vectors):正交是垂直的另一种说法,两个向量夹角是 90 度,点积为0,\(x^Ty = 0\)。
根据毕达哥拉斯定理,如果向量 x 和 y 正交,那么:
或者
而
从上式也能得到 \(x^Ty = 0\),这里运用了一个转置的性质,多个向量和的转置等于它们转置的和,\((x+y)^T = x^T + y^T\)。
零向量和任意向量正交。
正交子空间
两个子空间正交意味着它们的任意向量都互相正交。
三维坐标系中的 xy、xz、zy 三个平面并不正交,因为它们有共同的交线,比如有向量既在 xy 平面上,又在 xz 平面上。
行空间和零空间正交,它们都位于 \(R^n\) 空间之内,它们的维度之和为 n(注意,这并不是说行空间和零空间构成了整个 \(R^n\) 空间),我们把这种关系称为正交补(Orthogonal Complement),即行空间和零空间互为正交补,列空间和左零空间互为正交补,正交补意味着和行空间正交的所有向量都在零空间中,反之亦然。
如何判断 Ax = b 是否有解
这里要用到一个关键矩阵,\(A^TA\)。
\(A^TA\) 有以下性质:
A 是个 mxn 矩阵,\(A^TA\) 是个 nxn 的对称矩阵,但不一定可逆。
\(A^TA\) 的秩等于 A 的秩,\(A^TA\) 的零空间和 A 的零空间相同。
(两个矩阵乘积的秩不大于这两个矩阵各自的秩)
当且仅当 A 的各列线性无关时,\(A^TA\) 可逆
在 Ax = b 左右两侧同时乘以 \(A^T\),得到:\(A^TAx = A^Tb\)
投影(Projection)
现在在二维空间中有两个向量 a 和 b,我们想把 b 投影到 a 上,也就是说,从 b 出发,做一条垂线到 a 上,垂足为 p,那么 p 就是 b 在 a 上的投影。
用 e 表示 b 到 p 这个垂直向量,那么 e 必须和 a 正交,\(a^Te = 0\),同时,\(e = b - p\),并且 p 是 a 的一个倍数,\(p = xa\),x 代表倍数,因此,\(a^T(b - xa) = 0\),求出 x,就能得到 p。
由上述方法可以得到:
(实际上,用几何的方法也能得到这个结果,用几何的方法求x, \(x = \frac{\|b\|\cos\theta}{\|a\|}\),和上面的结果实际上是等价的。)
投影 p 就是某个投影矩阵 P 作用在向量 b 上,在上面的例子中,投影矩阵为:
P 的列空间这就是 a 所在的直线,P 的秩为 1。
投影矩阵是对称的,\(P^T = P\),并且满足 \(P^2 = P\),即投影矩阵自乘仍然等于它本身。
扩展到 n 维空间
上述例子考虑的是二维空间中的投影。
考虑更高维的情况,并结合判断 Ax = b 是否有解这个问题一起来看,假设有一个矩阵 A 表示一个平面,如果我们想判断 Ax = b 是否有解,实际上是在判断 b 是否在 A 平面上,我们可以求 b 的投影,如果 b 在 A 平面上,那么 b 的投影就是它本身。
b 在平面 A 上的投影 p 可以表示为 A 的某个线性组合,\(p = A\hat{x}\),因此,求 x 的方程就变成了 \(A^T(b - A\hat{x}) = 0\),这其实和上面提到的 \(A^TAx = A^Tb\) 是等价的。
垂直于 A 的向量 e 位于 A 的左零空间。
系数向量 \(\hat{x}\),投影向量,投影矩阵分别为: $$ \hat{x} = (A^TA)^{-1}A^Tb \ p = A\hat{x} = A(A^TA)^{-1}A^Tb \ P = A(A^TA)^{-1}A^T \ b = p + e \ e = (I-P)b \ $$
如果此时 A 是一个可逆矩阵,那么投影矩阵 P 就是单位矩阵 I。
\(P^T = P\),\(P^2 = P\),这两个性质仍然满足。
b 投影到左零空间的向量为 e,投影矩阵为 I-P,同样满足上述投影矩阵的性质。
(注意:A 中包含的都是线性无关的基向量)
例子:最小二乘法(Least Squares)拟合直线
假设有三个点 (1,1),(2,2),(3,2),我们想用一条直线 b = c + dt 来拟合出一条直线。
将点代入,可列出方程组
将方程组改写为 Ax = b 的形式:
这个方程组有可能无解,因为这些点可能不都在拟合的直线上。
我们的目的是求 c 和 d 的最优解,使得拟合直线尽可能接近这些点,也就是让总误差最小。
总误差是所有误差的平方和,“最小二乘”这个名称就是使误差的平方和最小化的意思。
什么情况下误差最小?当 Ax 为 b 在 A 上的投影时,误差最小,此时 e 和 A 垂直,因此,解方程 \(A^TAx = A^Tb\)。
从微积分的角度,求出使误差最小的 c 和 d(c 和 d 组成了 x),对 \(\|Ax-b\|^2\) 分别关于 c 和 d 求偏导数,并令偏导数为0,也能得到 \(A^TAx = A^Tb\) 这组方程。
最优直线为
正交基和正交矩阵
标准正交向量(Orthonormal Vectors):向量不仅正交,而且每个向量的长度为1。
标准正交基(Orthonormal Basis):一组标准正交向量作为空间的基向量(基向量的数量不一定和空间维度相同,比如在 \(R^3\) 中,我需要一个二维子空间,那么我只需要两个标准正交向量作为基向量)。
用 Q 表示标准正交向量组成的矩阵(不一定是方阵),\(Q^TQ\) 是 单位矩阵 I,如果 Q 是方阵,Q 本身就是 I。
正交矩阵是由标准正交向量组成列向量的方阵,\(Q^T = Q^{-1}\)。
前面提到的置换矩阵就是正交矩阵。
旋转矩阵也是正交矩阵,例如二维空间中的旋转矩阵:
格拉姆-施密特(Gram-Schmidt)正交化过程:将一组线性无关的向量转换为一组标准正交向量。
施密特正交化得到的正交向量会让计算变得简单,比如计算投影的方程 \(A^TA\hat{x} = A^Tb\) 会变成 \(Q^TQ\hat{x} = Q^Tb\),进而变成 \(\hat{x} = Q^Tb\),第 i 个基方向上的投影就是 \(\hat{x_i} = q_i^Tb\)。
格拉姆-施密特正交化
有三个线性无关的向量 a,b,c,我们想把它们转换为标准正交向量。
- 先求出三个正交向量 A,B,C,
- 然后将其标准化为单位向量 q1,q2,q3。
直接将向量 a 作为 A。
求 B 的方法是对 b 做投影,先将 b 投影到 A 上,得到投影向量 p,然后用 b 减去 p,得到向量e,e 就是向量 B。
可以这么理解,这是将 b 在 A 方向上的分量减去,只保留垂直于 A 方向上的分量。
向量 C 需要将 c 在 A 和 B 方向上(注意是 A 和 B,不是 a 和 b)的分量都减去,只保留垂直于 A 和 B 方向上的分量。
最后,将 A,B,C 分别除以自身长度标准化为单位向量。
经过施密特正交化后的向量和变换前的向量位于同一个列空间。
施密特正交化过程可以和前面的矩阵分解联系起来(A = LU)
R 是一个上三角矩阵。
行列式(Determinant)
det(A) 或 |A| 表示矩阵 A 的行列式,A 必须是方阵。
矩阵可逆,行列式不为零;矩阵不可逆,行列式为零。
2x2 行列式的计算方法:
行列式的十个性质
性质1,单位矩阵的行列式值为 1。
性质2,交换行,行列式的值符号会取反(置换矩阵的值为 1 或 -1,取决于交换次数)。
性质3,对于任一行,有以下性质: $$ \begin{vmatrix} ta & tb \ c & d \ \end{vmatrix} =t \begin{vmatrix} a & b \ c & d \ \end{vmatrix} $$
可以得出,\(det(2A) = 2^n det(A)\)。
性质4,如果两行相同,行列式的值为0。
性质5,消元不会改变行列式的值。
性质6,如果有一行是全0,行列式的值为0。
性质7,三角矩阵行列式的值等于对角线元素的乘积(无论是上三角矩阵还是下三角矩阵)。
性质8,当且仅当 A 为奇异矩阵时(不可逆),行列式的值为0,当且仅当 A 为非奇异矩阵时(可逆),行列式的值不为0。 - 如果矩阵奇异(不可逆),消元后会出现全 0 行 - 如果矩阵非奇异(可逆),消元后会成为上三角矩阵或者对称矩阵。
我们对 2x2 矩阵做一次消元:
性质9,\(det(AB) = det(A) * det(B)\)。由此可以得到一系列结论,\(det(A^{-1}) = 1/det(A)\),\(det(A^2) = det(A)^2\)。
性质10,\(det(A^T) = det(A)\),以上所有性质对列也是成立的。
行列式的求解公式
按照这个规律,3x3 行列式最终可以拆分为 27 个行列式,最终实际产生作用的行列式的每行和每列都只有一个元素不为0。
求解 nxn 行列式的通用公式为:
代数余子式(Cofactor)是把每项除了第一个乘数以外剩余的乘积提取出来,用 \(C_{ij}\) 表示 \(a_{ij}\) 的代数余子式,那么上面的行列式可以改写为:
\(C_{11}\) 相当于把第一行第一列去掉,剩余部分的行列式就是 \(C_{11}\)。
行列式的求和公式可以从任意一行展开,例如可以计算 \(a_{21}C_{21}+...+a_{2n}C_{2n}\)。
代数余子式将每项的计算拆解为递归计算的过程,将一个大行列式的计算不断拆解为小行列式的计算,直到拆解到 2x2 行列式为止。
逆矩阵公式
2x2 矩阵的求逆公式:
其中,C 是 A 的代数余子式矩阵,\(C^T\) 叫做伴随矩阵(Adjoint Matrix)。
如果计算 \(AC^T\) 就会发现,\(AC^T\) 的对角线元素都等于 A 的行列式值,其余元素都为0,因此,\(AC^T = det(A)I\),从而得到 \(A^{-1} = \frac{1}{det(A)}C^T\)。
从这里也能看出来,A 的某一行向量和其他任意行的代数余子式向量是正交的。
克拉默法则
Ax = b 有唯一解的条件是 A 可逆,此时 \(x = A^{-1}b = \frac{1}{det(A)}C^Tb\)。
\(C^T\) 的每个元素都是一个代数余子式,\(C^T\) 的一行和 b 的点积可以看作是求某个矩阵的行列式值,因此,我们将 x 的元素表示为这种形式: